¿Cuántos vacíos hay en la teoría de cuerdas?

Fuente: Francis (th)E mule

La teoría de cuerdas, teoría M, teoría F, o como quieras llamarla, pretende describir la realidad a muy alta energía, la escala de Planck. La física a baja energía que nos rodea todos los días e incluso la física a “altas” energías en los grandes colisionadores de partículas corresponden al vacío de la teoría ST/M/F, pues son energías ridículas comparadas con la energía de Planck. Como vivimos en el vacío de la teoría, una cuestión importante es saber si el número de vacíos posibles en la teoría ST/M/F es finito o infinito, y en caso de que sea finito, obtener una estimación de su número.
La conjetura “oficial” es que hay un número finito de vacíos posibles, pero no está demostrado; en cuanto a la estimación de dicho número hay muchas opciones que van desde los 10²⁰ vacíos de Douglas, pasando por los 10¹²⁰ de Weinberg, llegando hasta los 10⁵⁰⁶ de Bousso-Polchinski. Por concretar un número “razonable” se suele decir en casi todo los sitios que son unos 10⁵⁰⁰ vacíos (porque es un número redondo y queda muy bonito). Un número inimaginable que nos lleva al problema del paisaje (landscape), quizás la teoría ST/M/F es una teoría de todas las cosas posibles, incluyendo todo lo que nos rodea.
Quizás conviene que recordemos cómo se cuentan los vacíos y por qué es tan difícil estimar cuántos son. Me ha recordado este problema la lectura de Tamar Friedmann, Richard P. Stanley, “The String Landscape: On Formulas for Counting Vacua,” Accepted in Nucl. Phys. B, arXiv:1212.0583, Subm. 3 Dec 2012. Esta entrada le parecerá muy técnica a algunos y muy ligera a otros. Explicar estas cosas es difícil y yo soy un humilde aprendiz.
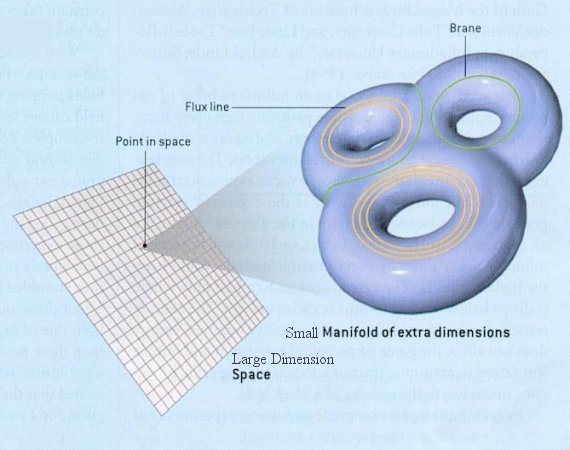
En la teoría de (super)cuerdas el espaciotiempo tiene 10 dimensiones (10D), separadas en dos partes, 4 del espaciotiempo de Minkowski ordinario (4D) y 6 dimensiones extra (6D), que no notamos porque son compactas (“muy pequeñas”). La forma de las 6 dimensiones extra debe corresponder a una solución para el vacío de las ecuaciones de Einstein de la gravedad. Si la variedad 6D se entiende en variable real, la única solución es un espaciotiempo plano. Sin embargo, si se considera la variedad 6D como una variedad en variable compleja de dimensión tres, existen soluciones de las ecuaciones de Einstein para el vacío, llamadas variedades de Calabi-Yau (CY); Calabi conjeturó su existencia y Yau la demostró (recibió por ello la Medalla Fields) usando un método no constructivo.
¿Cuántas variedades de CY hay? El propio Yau ha conjeturado que hay unas 30.000 variedades CY (por ordenador se han calculado unas 15.000), pero quizás haya más; sin embargo, muchos matemáticos, como Reid, creen que hay un número infinito. Por tanto, a día de hoy nadie sabe cuántas variedades de CY existen y no se puede descartar que su número sea infinito. Lo importante que hay que recordar es que esto no importa, como veremos en lo que sigue.
Cada variedad CY tiene una serie de parámetros continuos, los módulos (moduli), que especifican su forma y de tamaño; no es una variedad CY, pero un cilindro 2D (un dónut) está definido por dos radios que determinan su forma y su tamaño, que serían sus módulos. En teoría cuántica de campos (y la teoría de cuerdas lo es) los módulos corresponden a campos escalares y a sus correspondientes partículas; mucha gente se imagina “vibraciones” de las cuerdas a lo largo de un módulo como partículas del campo asociado. ¿Cuántos módulos tiene una variedad CY típica? No se sabe, pero se cree que es un número finito y pequeño. Se conocen variedades de CY con 101 módulos y otras con uno solo, pero la mayoría parece tener decenas de módulos.
El vacío de la teoría corresponde al estado de energía mínima. Para calcular este mínimo se suele recurrir al flujo del campo de cuerdas a través de la compactificación en la variedad de CY, aunque hay algunos autores como Banks que consideran que este procedimiento no es adecuado. Este proceso requiere minimizar una integral sobre la variedad parametrizada por los módulos. La geometría complicada de estas variedades hace que tengan muchos mínimos para el flujo (pero como son compactas dicho número es finito); el flujo del campo en estos mínimos puede ser estable, metaestable o inestable; los vacíos de la teoría se supone que corresponden a los mínimos estables (aunque algunos teóricos de cuerdas también consideran los metaestables). Además, los valores del flujo del campo están cuantizados (puede haber 1, 2, 3, …, unidades de flujo, pero no puede haber 1,46 o pi unidades de flujo). Contar el número de vacíos requiere contar cuántas variedades de CY tienen mínimos estables y cuántos valores discretos pueden tener los flujos en dichas variedades CY. La tarea no es fácil.
La labor de contar el número de vacíos parece casi imposible dada nuestra ignorancia sobre las variedades CY, sin embargo, hay un truco muy curioso, utilizar un potencial efectivo que gobierne la física a baja energía (esta idea tiene detractores pues no da cuenta de los efectos cuánticos de la gravedad, que es tratada de forma clásica). El potencial efectivo será resultado de la rotura de la supersimetría en la teoría de cuerdas. La ventaja de usar un potencial efectivo es que se pueden usar ideas de cosmología para restringir los posibles vacíos estables de la teoría. El potencial efectivo se comporta como un “paisaje de cuerdas” (string landscape) y los mínimos estables del potencial serían como mínimos “geométricos” en dicho “paisaje.” Estos mínimos conforman un conjunto “discreto” de parámetros efectivos a baja energía y tiene sentido aplicar técnicas estadísticas para estimar su número.
La forma general del potencial efectivo a baja energía se puede conjeturar (hay varias propuestas o técnicas para hacerlo que se suelen llamar técnicas de estabilización del vacío). Los posibles mínimos del potencial efectivo se corresponden con propiedades geométricas de la variedad de Calabi-Yau, como el número de ciclos (una generalización del número de Betti en las superficies); de esta forma se obtienen conjuntos para los posibles vacíos del flujo del campo de cuerdas que se pueden contar utilizando herramientas geométricas. Se conocen varias técnicas de estabilización del vacío y cada una ofrece una cuenta diferente para el número de vacíos; aunque estas técnicas no son aplicables a todas las teorías de cuerdas (recuerda que hay cinco teorías), como éstas son duales entre sí (representan la misma física), se supone que las cuentas deberían coincidir para todas ellas. Los primeros trabajos que contaron el número de vacíos se centraron en las teorías de cuerdas IIB y IIA, pero en los últimos años también se han aplicado a las cuerdas heteróticas. El problema es que los números no suelen coincidir en las diferentes teorías de cuerdas, lo que disgusta a algunos expertos.
La técnica más famosa para contar vacíos, aplicada a la teoría de cuerdas IIB, fue introducida por Kachru, Kallosh, Linde y Trivedi, por eso se llama técnica KKLT. Utilizando técnicas de D-branas, KKLT logran estabilizar los vacíos restringiendo los módulos de tamaño de las variedades de CY; lo sorprendente es que su idea también restringe de forma “milagrosa” los módulos de forma. Todo ello les permite contar el número de vacíos posibles. Obviamente, la técnica KKLT es solo un “modelo de juguete” de cómo se pueden estabilizar los módulos. ¿Cuántos vacíos hay según la técnica KKLT en una teoría de cuerdas IIB? El artículo técnico ofrece varios valores, dependiendo de ciertos detalles técnicos del modelo efectivo utilizado, unos 10³⁰⁷, 10³⁹⁸, o 10⁵⁰⁶ vacíos. Que el mismo artículo/técnica ofrezca valores tan variados puede hacer sospechar de la calidad del resultado, por ello muchos expertos afirman que KKLT estimaron unos 10⁵⁰⁰ vacíos. Un número “redondo” donde los haya.
¿Cuántos vacíos hay la teoría M en once dimensiones? En esta teoría las 7 dimensiones extra (7D) se compactifican utilizando una variedad con grupo de holonomía G2. Estas variedades son mucho más díficiles de estudiar que las variedades CY y se conocen poco sus propiedades. También se ha conjeturado que hay un número finito, pero sin demostración. Las variedades G2 tiene módulos y se han desarrollado técnicas de estabilización del vacío que permiten contar su número. De nuevo, se obtienen muchos.
¿Cuántos vacíos hay en la teoría F en doce dimensiones? En esta teoría las 8 dimensiones extra (8D) se compactifican en una variedad de Calabi-Yau con 4 dimensiones complejas. Muchas de las técnicas de estabilización de vacíos para la teoría de cuerdas se pueden utilizar en este contexto. Aunque me repita, de nuevo, se obtienen muchos.
¿Realmente el problema del “paisaje” es un problema en la teoría ST/M/F? Muchos físicos interpretan este problema como una señal de que la teoría ST/M/F no puede ser la respuesta correcta (promete mucho pero no ayuda nada de nada). Sin embargo, muchos físicos de cuerdas argumentan que el problema del paisaje quizás no es un problema. Quizás el problema es que no conocemos las técnicas matemáticas adecuadas para estabilizar el vacío y estamos dando palos de ciego con nuestras torpes técnicas actuales. Quizás la teoría ST/M/F tiene un único vacío y predice el universo que conocemos. El único universo que conocemos. Quizás, el único universo posible.
¿La teoría ST/M/F es metafísica? ¿Es solo matemática? ¿Hay física en la teoría ST/M/F?
Recomiendo leer a T. Banks, “The Top 10^{500} Reasons Not to Believe in the Landscape,” arXiv:1208.5715, 28 Aug 2012. Y por supuesto, la opinión contraria de Lee Smolin, “A perspective on the landscape problem,” arXiv:1202.3373, 15 Feb 2012.