Mecánica Cuántica, realismo y localidad

Fuente: Neofronteras
 
Un experimento elimina, al parecer, el realismo sólo para una clase grande de teorías no locales.

Esquema del experimento. Fuente: Sonja Franke-Arnold.

Desde que la Mecánica Cuántica (MC) fue formulada, algunos físicos de renombre como el propio Albert Einstein se sintieron incómodos con algunos de sus detalles. Uno de esos aspectos era la posibilidad de que dos partículas estuvieran entrelazadas de tal modo que una medida sobre una de ellas parecía influir en la otra en experimentos de tipo EPR (ver referencias al final).
La MC es contraria a la intuición que hemos adquirido en el mundo macroscópico por dos particularidades principalmente. Uno esperaría que toda teoría clásica fuera “local”, es decir, que un objeto puede ser influido solamente por su inmediata vecindad. La segunda es que debe ser “realista”, lo que significa que los objetos tienen unas propiedades definidas que son independientes de si lo estamos midiendo o no. La MC parece violar esas condiciones. Así por ejemplo, si dos fotones correlacionados se separan una distancia suficiente, basta hacer una medición sobre uno de ellos, entonces queden fijadas las propiedades del otro en un proceso que parece darse a mayor velocidad que la luz.
En el pasado se propuso que la MC no era una teoría completa y que debía de haber una teoría clásica de variables ocultas, aún por formular, que explicara lo observado, teoría que además sería local y realista. Aunque nadie ha llegado a expresar tal teoría se han diseñado experimentos y desarrollado una base teórica que permite pensar sobre el problema.
Las rarezas de la MC fueron expresadas matemáticamente por John Bell en sus famosas desigualdades. Bell mostró que una particular combinación de medidas realizadas sobre un par de partículas preparadas del mismo modo producirían unos resultados que cumplirán unas desigualdades siempre y cuando la teoría fuese realista y local.
De este modo se pueden diseñar experimentos que traten de medir esas desigualdades para poner a prueba la MC. En este tipo de experimentos se suele medir la polarización de pares de fotones cuidadosamente preparados a lo largo de diferentes direcciones y calcular las correlaciones entre ellos. Esto ya fue realizado por Stuart Freedman y John Clauser en los setenta, y por Alain Aspect en los ochenta, comprobándose la violación de las desigualdades de Bell. Los resultados, por tanto, confirmaron la MC y su sacrificio del realismo local.
Pero las hipotéticas teorías de variables ocultas se resisten a desaparecer debido a que hay tres lagunas que permiten explicar las violaciones de realismo local observadas con hipotéticas teorías realistas locales. Estas lagunas tienen que ver con la localidad, si no hay suficiente distancia que separe las partículas; la libertad a la hora de elegir un conjunto de medidas, de tal modo que esta elección pudiera estar influida por variables ocultas; y el muestreo, ya que una fracción pequeña de los objetos observados puede que no estén adecuadamente representando a todos los demás debido a problemas de detección.
La primera laguna ya fue eliminada en el pasado aumentando la distancia, indicándose una violación del realismo local. Mientras que la tercera fue superada en un experimento con iones para los que hay buena eficiencia a la hora de su detección.
Recientemente se realizó un experimento de Bell para fotones correlacionados separados 144 km entre sí generados por un diodo láser. Esa distancia es la que media entre la isla de la Palma y Tenerife, que fue recorrida libremente por los fotones a través de la atmósfera. En este experimento se midió que la Naturaleza viola el realismo local con una estadística muy buena de 16 desviaciones estándar. Se trataba de evitar la primera laguna con esos 144 km y un retardo realizado con una fibra óptica de 6 km y la segunda usando estados elegidos aleatoriamente. Descubrieron que, pese a todo, las medidas eran explicadas por la MC violándose en realismo local. Con esto se reduce el número de posibles teorías de variables ocultas realistas y locales que pudieran explicar las correlaciones observadas. Estos investigadores esperan que en unos cinco años se pueda eliminar en un experimento esas tres lagunas simultáneamente.
Aunque hay otras soluciones. En 2003 Anthony Leggett de la Universidad de Illinois trató de restaurar el realismo a costa del sacrificio de la localidad. Si dos entidades cuánticas pueden comunicarse a través de una señal instantánea (no localismo) entonces quizás sea posible que cada una de ellas tenga unas propiedades definidas (realismo). Este escenario superaría el test de Bell, pero, ¿describe el mundo cuántico?
Durante años, físicos de Austria, Suiza y Singapur han tratado de responder a esa la pregunta. En lugar de medir estados de polarización lineal para hacer el test de Bell se usan polarizaciones elípticas que son combinaciones de estados de polarización lineal y circular. Incluso asumiendo que los fotones entrelazados pudieran responder instantáneamente a la situación del otro, las correlaciones entre estados de polarización violaban las desigualdades de Leggett. La conclusión era que incluso admitiendo una comunicación instantánea no era posible explicar el entrelazamiento y por tanto no era posible mantener el realismo.
Ahora, otro experimento realizado por Sonja Franke-Arnold y sus colaboradores de las universidades de Glasgow y Strathclyde muestra que los fotones entrelazados muestran correlaciones más fuertes que las permitidas a partículas con propiedades individuales bien definidas, incluso si se les permite comunicarse instantáneamente. Pero en lugar de usar la polarización, midieron las propiedades del momento orbital angular del fotón.
Este momento orbital angular puede ser comprendido imaginando las ondas como si estuvieran retorcidas alrededor del eje del haz. Puede ser representado como una hélice simple (un sacacorchos), una doble hélice o hélices más complejas según se aumenta el momento angular. Estos investigadores se centraron en la hélice doble.
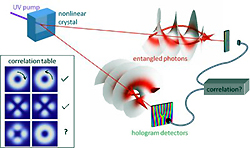
En concreto, usaron un láser ultravioleta que disparaban contra un cristal óptico diseñado para dividir los fotones en pares entrelazados de fotones infrarrojos. Estos iban hacia hologramas controlados computacionalmente que filtraban estados de momento angular orbital complementario. Los fotones que finalmente se obtenían eran contados uno a uno por detectores especiales.
La MC así como las proposiciones de Bell y Leggett dicen cómo deben ser las correlaciones entre dos fotones entrelazados, uno con momento orbital angular a favor de las agujas del reloj y otro en contra. Cuando estos físicos desalinearon deliberadamente los hologramas, las medidas decían que las coincidencias estaban estadísticamente de acuerdo con la propuesta de Leggett, pero no con las predicciones de la MC.
Según estos investigadores se trata de un resultado filosófico. Las partículas entrelazadas no pueden describirse como entidades individuales incluso si se tiene en cuenta una conexión “telepática” entre cada miembro del par.
Simon Gröblacher, de la Universidad de Viena y un experto en el campo, dice que este experimento elimina el realismo sólo para una clase grande de teorías no locales, mientras que otras no son descritas por las desigualdades de Leggett.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=3344
Fuentes y referencias:
Artículo original.
Noticia en Physics world
Artículo original.
Consiguen estados cuánticos entrelazados en un chip.
Realizada la teleclonación cuántica.
La mecánica cuántica pasa otra prueba.
Entrelazamiento cuántico y libre albedrío.
Localidad e incertidumbre.

 Versión para imprimir

Salvo que se exprese lo contrario esta obra está bajo una licencia Creative Commons.

La red de transporte interplanetario

Fuente: La pizarra de Yuri

Desarrollada teóricamente a finales del siglo XIX y resuelta en los últimos años del XX,
la Red de Transporte Interplanetario resuelve el problema de viajar entre mundos
con un coste energético ridículamente bajo. Sólo es un poco más lenta.

Lanzamiento de la nave espacial interplanetaria New Horizons
con destino a Plutón-Caronte y el cinturón de Kuiper,
a bordo de un cohete Atlas V-Star 48B, el 19 de enero de 2006.
Llegará en junio de 2015, tras un viaje de cinco mil millones de kilómetros.
Los cohetes sólo actúan durante los primeros minutos;
el resto del viaje carece de propulsión autónoma. (NASA)

La nave New Horizons durante su ensamblaje final. Cuenta con dieciséis motores de 4,4 newtons para correcciones de trayectoria y doce de 0,9 newtons para el control de actitud, pero ningún impulsor principal, al igual que el resto de naves espaciales humanas del presente y del futuro próximo. Foto: NASA. (Nueva ventana o pestaña para ampliar)

A pesar de lo que se pudiera concluir tras ver muchas pelis de ciencia-ficción, las naves espaciales carecen generalmente de propulsión propia. Sólo llevan una pequeña cantidad de combustible y unos motorcitos minúsculos para realizar ocasionalmente maniobras de corrección de trayectoria, casi siempre con el propósito de mantener la posición. Así es tanto en los satélites como en las sondas de espacio profundo, así ha sido durante toda la Era Espacial, sigue siéndolo en la actualidad y seguirá siéndolo durante una buena temporada. No hacemos vuelo libre por el espacio, sino que describimos órbitas y realizamos triquiñuelas aprovechando los efectos de la gravedad y la velocidad, en una especie de billar cósmico.

En cierto sentido, una nave espacial se parece mucho más a un velero gravitacional que a un navío a motor. Esos enormes cohetes que vemos encenderse con poderosos rugidos y llamaradas sólo están para sacar la nave del pozo gravitatorio terrestre. Tragan combustible a mares y se agotan enseguida. Al poco del lanzamiento se van apagando y desprendiendo, normalmente por fases, y unos pocos minutos después se acaban todas y liberan la nave. En un lanzamiento sencillo a la órbita baja terrestre, esto está visto para sentencia en menos de diez minutos. Por ejemplo, la impulsión para una Soyuz con destino a la Estación Espacial Internacional termina a los nueve minutos; el resto del viaje se completa por la órbita, conservando la velocidad adquirida durante el lanzamiento sin propulsión significativa adicional.

Para ir más lejos, lo que requiere ir algo más rápido, se suele utilizar una última fase que se enciende de nuevo al llegar a un cierto punto de la órbita para darle un último empujón. Esto es lo que hace, por ejemplo, la etapa Fregat de las Soyuz o la S-IVB de los Saturno V que los estadounidenses usaron para llevar a la humanidad a la Luna. Pero incluso estas últimas aportaban una impulsión adicional de apenas seis minutos. Quien desea ir a Venus o Marte, pongamos por caso, lo hace de manera muy parecida; en este último enlace puede verse cómo un viaje a Marte sólo está propulsado seriamente al principio, durante unos catorce minutos y pico en total, de los siete meses que dura. A partir de ahí sólo actuarán los motores de maniobra, muy de tarde en tarde, para realizar pequeñas correcciones o forzar la inyección final en la órbita marciana.

Esto es posible porque en el espacio no se produce arrastre aerodinámico, dado que no hay aire. Una nave colocada en una órbita estable a una velocidad determinada tiende a mantener esta velocidad en virtud de la primera ley de Newton. Como decía al principio, después se pueden utilizar trucos para aumentar (o reducir) esta velocidad, del tipo de la asistencia gravitatoria. El vuelo espacial es un juego de trayectorias y velocidades. Sí, como en el billar.

Venera-7, la primera nave espacial humana que aterrizó con bien en otro mundo. Se posó cerca de Safo de Venus, al sur de la Planicie de Ginebra, siendo las 05:34:10 GMT del 15 de diciembre de 1970; acaba de hacer cuarenta años.

Vuelo interplanetario.

Para viajar entre astros hay que tener claros dos conceptos fundamentales: la velocidad de escape y la órbita de transferencia de Hohmann.  Dicho en plan sencillo, la velocidad de escape es lo rápido que hay que ir para escapar de la atracción gravitatoria de la Tierra o cualquier otro astro. Más técnicamente, se define como la velocidad a la que la energía cinética de la nave contrarresta a la energía potencial gravitatoria resultante de la interacción entre la nave y el astro. La velocidad de escape es independiente de la masa del objeto que escapa: da igual si tu nave pesa un kilo o un millón de toneladas (en este último caso necesitarás más energía para acelerarla hasta ese punto, pero la velocidad de escape no varía). Por el contrario, es dependiente de la distancia entre la nave y el astro. Por ejemplo, si la nave estuviera situada sobre la superficie terrestre, la velocidad de escape sería de 11,2 km/s (40.320 km/h); sin embargo, en la órbita baja desciende a 10,9 km/s (39.240 km/h) y a nueve mil kilómetros de distancia, cae a algo menos de 7,1 km/s (25.560 km/h). De hecho la velocidad de escape depende sólo de la distancia entre ambos objetos y la intensidad del campo gravitatorio en ese punto, y se describe con la ecuación ve = (2gr)½, donde g es el campo gravitatorio y r la distancia que separa sus centros de masas. La velocidad de escape es un fenómeno que se deriva del principio de la conservación de la energía.

Hablar de velocidad de escape a pelo no tiene demasiado sentido. Hablamos siempre de velocidad de escape desde algún sitio con respecto a algo: la Tierra, el Sol, la Luna, Saturno, el centro de la galaxia, lo que sea. Por ejemplo: ya hemos dicho que la velocidad de escape desde la órbita baja terrestre con respecto a la Tierra son 10,9 km/s. Pero la velocidad de escape desde este mismo lugar con respecto al Sol asciende a 42,1 km/s (151.560 km/h). Esto quiere decir que una nave situada más o menos por donde la Estación Espacial Internacional necesita ir a algo menos de cuarenta mil kilómetros por hora para escapar de la gravedad terrestre, pero tendría que viajar a más de ciento cincuenta mil para zafarse de la del Sol desde el mismo punto, por ejemplo con el propósito de efectuar un viaje interestelar. Evidentemente, los científicos e ingenieros espaciales tratan de jugar con las distancias y velocidades para conseguir el máximo ahorro de energía, de tal modo que estos viajes sean posibles con los motores y las cantidades de combustible que somos capaces de manejar.

Cuando una nave espacial alcanza la velocidad de escape entra en órbita de escape, que es una trayectoria parabólica de mínima energía (o sea, una órbita de Kepler con excentricidad 1) que la lleva hacia el infinito mientras la velocidad con respecto al objeto del que ha escapado tiende a cero. Y yendo un poco más deprisa, se puede pasar también a una trayectoria hiperbólica (es decir, una órbita de Kepler con excentricidad mayor que 1). Así se puede viajar hacia cualquier lugar del cosmos sin necesidad de llevar propulsión todo el tiempo.

Sin embargo, se intuye fácilmente que hace falta mucha energía para alcanzar estas velocidades. En torno a 1925 un ingeniero alemán llamado Walter Hohmann, inspirado por la lectura de obras de ciencia ficción, intentó encontrar una manera de reducirlas. También por las mismas fechas, un matemático soviético de nombre Vladimir P. Vetchinkin estuvo estudiando la cuestión. Resulta difícil determinar cuál dio con la solución primero, pero ambos alcanzaron las mismas conclusiones, que en Occidente se denominan las órbitas de Hohmann y en el espacio ex-soviético, de Hohmann-Vetchinkin.

Una órbita de Hohmann (o Hohmann-Vetchinkin) no es una órbita típica de escape, parabólica o hiperbólica, sino un tipo particular de órbita elíptica. Una órbita elíptica es una órbita de Kepler con excentricidad menor que 1, hasta la órbita circular, con excentricidad cero (aunque normalmente esta última se denomina órbita circular a secas). Simplificando, es cualquier órbita que no escapa de un astro determinado (aunque puede alejarse bastante de él). En consecuencia, la velocidad (y por tanto la energía) necesaria para establecerse en ella resulta significativamente menor. Hay varios tipos posibles de órbitas elípticas, algunos de ellos muy prácticos, desde la conocida Molniya hasta la más rara órbita tundra.

Órbita de transferencia Hohmann-Vetchinkin (2) entre una órbita baja (1) y otra geoestacionaria (3).

Una órbita de transferencia Hohmann (o Hohmann-Vetchinkin :-D ) es una órbita elíptica parcial que sirve para saltar entre dos órbitas circulares situadas a distinta distancia. Por ejemplo, en la imagen de la izquierda la vemos utilizada para conmutar entre una órbita baja (1) y una órbita geoestacionaria (3) en ambos casos con la Tierra en el centro; es el tramo amarillo (2). Para realizar esta maniobra, sólo necesitamos dos impulsos, uno a la entrada y otro a la salida. La gracia radica en que estos dos impulsos consumen bastante menos energía que la necesaria para alcanzar la velocidad de escape (y no digamos si encima hay que abandonarla en destino). La desgracia, que resulta en un recorrido más largo que la trayectoria parabólica y mucho más largo que la hiperbólica.

Pero en la mayoría de casos, resulta la manera energéticamente más económica de viajar entre dos órbitas circulares que no tienen por qué pertenecer al mismo astro (si bien la mecánica específica se complica un poco más en este último caso). Es decir: podemos salir de una órbita circular alrededor de la Tierra y acabar en una órbita circular alrededor de Venus o Marte o el Sol o cualquier otro lugar con menos coste energético que tratando de alcanzar la velocidad de escape. Dicho de otra manera, es la forma más eficiente de trasladar una nave espacial entre dos órbitas distintas. Bajo determinadas circunstancias, la transferencia bi-elíptica puede optimizar aún más el coste energético.

Y es que en las naves espaciales del presente (y del futuro próximo) el problema fundamental es el coste energético. Cuanta más energía necesite una nave espacial para completar su viaje, requerirá más combustible y más motores, es decir más masa y volumen. O sea que tendrá que ser una nave más grande, más difícil de construir y con un coste económico mucho mayor. A partir de cierto punto, el proyecto se tornará irrealizable. Por eso el balance energético de una misión espacial es tan importante. Cualquier cosa que lo mejore no sólo reduce el dinero a gastar, sino que abre puertas al futuro que de otra manera no serían posibles en la práctica.

Plan de vuelo Tierra-Venus para la nave interplanetaria soviética Venera-5, utilizando una órbita de transferencia Hohmann-Vetchinkin de tipo I durante la ventana de enero de 1969.

Los puntos de Lagrange.

Estatua a Joseph-Louis de Lagrange (Giuseppe Luigi Lagrangia) en Turín.

Y ahora vamos a hacer un inciso, que resulta imprescindible para poder continuar. Érase una vez que se era un matemático ítalofrancés llamado Joseph-Louis de Lagrange, que trabajaba en el problema newtoniano de los tres cuerpos; como puede suponerse fácilmente, una extensión del problema de los dos cuerpos. :-D Dicho a lo fácil, esto del problema de los tres (o más) cuerpos estudia cómo se influyen mutuamente tres (o más) cuerpos que interaccionan gravitacionalmente entre sí. Por ejemplo, el sistema Sol-Tierra-Luna. O el Tierra-Venus-nave espacial, por decir otro.

Ciento ochenta y siete años antes del primer viaje a la Luna, este señor Lagrange dedujo matemáticamente una cosita interesante. Como la Wikipedia lo explica bastante bien, vamos a citarla:

En 1772, el matemático ítalo-francés Joseph-Louis Lagrange estaba trabajando en el célebre Problema de los tres cuerpos cuando descubrió una interesante peculiaridad. Originalmente, trataba de descubrir una manera de calcular fácilmente la interacción gravitatoria de un número arbitrario de cuerpos en un sistema. La mecánica newtoniana determina que un sistema así gira caóticamente hasta que; o bien se produce una colisión, o alguno de los cuerpos es expulsado del sistema y se logra el equilibrio mecánico. Es muy fácil de resolver el caso de dos cuerpos que orbitan alrededor del centro común de gravedad. Sin embargo, si se introduce un tercer cuerpo, o más, los cálculos matemáticos son muy complicados. Una situación en la que se tendría que calcular la suma de todas las interacciones gravitatorias sobre cada objeto en cada punto a lo largo de su trayectoria.

Sin embargo, Lagrange quería hacer esto más sencillo, y lo logró mediante una simple hipótesis: La trayectoria de un objeto se determina encontrando un camino que minimice la acción con el tiempo. Esto se calcula substrayendo la energía potencial de la energía cinética. Siguiendo esta manera de pensar, Lagrange reformuló la mecánica clásica de Newton para dar lugar a la mecánica lagrangiana. Con su nueva forma de calcular, el trabajo de Lagrange le llevó a plantear la hipótesis de un tercer cuerpo de masa despreciable en órbita alrededor de dos cuerpos más grandes que ya estuvieran girando a su vez en órbita cuasi circular. En un sistema de referencia que gira con los cuerpos mayores, encontró cinco puntos fijos específicos en los que el tercer cuerpo, al seguir la órbita de los de mayor masa, se halla sometido a fuerza cero. Estos puntos fueron llamados puntos de Lagrange en su honor.

–es.wikipedia, “Puntos de Lagrange“, redacción del 22/12/2010.

Dos cuerpos orbitando alrededor de su centro de masas común. El "problema de los dos cuerpos" que se pregunta por su comportamiento tiene solución relativamente sencilla mediante las integrales de movimiento; pero el "problema de los tres (o más) cuerpos", que surge al añadir otros, carece de una solución general y sólo se puede resolver para casos particulares. Estudiando esta cuestión, Lagrange dedujo sus puntos de Lagrange.

Los puntos de Lagrange para el sistema Sol-Tierra. Una nave espacial establecida en esas posiciones puede mantenerse en las mismas únicamente con energía de maniobra.

El primer punto de Lagrange, L1, es intuitivo y se da incluso aunque todos los cuerpos estén estáticos: en la línea imaginaria entre dos objetos con masa y por tanto gravedad, existe un lugar donde la atracción gravitatoria de uno cancela a la del otro. Un objeto de masa comparativamente despreciable situado justo en esa posición flotará entre ambos de forma indeterminada sin necesidad de ningún aporte de energía. En un sistema rotativo real como el Tierra-Luna, L1 está un poco desplazado y es levemente inestable, lo que se puede compensar con pequeñas maniobras.

L2 se encuentra en la misma línea que une a los dos objetos mayores, pero más allá de la menor. En este punto, la atracción gravitatoria de las dos masas principales entra en equilibrio con el efecto centrífugo de la masa menor que gira alrededor. L3 hace lo propio “al otro lado”, más allá de la masa mayor. Por su parte, L4 y L5 se encuentran en los vértices de los triángulos equiláteros con base común en la línea que une ambas masas mayores; es decir, que giran 60º delante y detrás del cuerpo con masa menor, según se ve desde la masa mayor. Podemos verlos en la imagen de la izquierda.

La gracia de los puntos de Lagrange es que una nave espacial establecida en los mismos puede mantenerse ahí indefinidamente con energía teórica cero, y en la práctica tan solo con un poco de energía de maniobra para L1, L2 y L3 y ninguna para L4 y L5. Estos puntos de estacionamiento, excelentes candidatos a convertirse en terreno para construir las casas de postas cósmicas, constituyen una especie de órbitas Lagrange-estacionarias –por analogía a las geoestacionarias– que están disponibles entre dos pares de astros cualesquiera.

Mapa de potencial en los puntos de Lagrange y órbitas posibles en torno a L1 y L2. Imagen: R. A. Tacchi en Interplanetary Transport Network, Universidad de California en Davis.

De hecho, por su estabilidad gravitacional, en los puntos de Lagrange cuarto y quinto tienden a acumularse ciertas cantidades de materia. Los asteroides troyanos se concentran alrededor de los puntos L4 y L5, y muy notablemente en los del sistema Sol-Júpiter (¿alguien ha dicho “estación minera”?). El sistema Tetis – Saturno presenta a su vez dos pequeñas lunas, Telesto y Calipso, en L4 y L5.; lo mismo ocurre con Helena y Pollux en los de Dione – Saturno. Marte presenta cuatro asteroides en L4 y L5 de Sol – Marte. En torno a los de Sol – Tierra podrían encontrarse las nubes de polvo de Kordylewsky. El planetoide compañero de la Tierra, 3753 Cruithne, intercambia energía con la misma a través de los lagrangianos Sol – Tierra; lo mismo sucede entre Epimeteo y Jano (Saturno), de manera mucho más notable.

Se sugiere que los puntos L1 y L2 de cualquier astro serían el lugar idóneo para instalar un ascensor espacial (específicamente los llamados ascensores espaciales lunares). La Sociedad L5, ahora parte de la National Space Society, viene proponiendo directamente la colonización de los puntos de Lagrange desde 1975. La Administración Obama acaricia la idea para el proyecto de enviar una misión tripulada a Marte. Tímidamente, la especie humana ya ha empezado a ocupar los lagrangianos L1 y L2 de Sol-Tierra con algunas naves científicas. Una característica peculiar de los puntos de Lagrange es que un objeto (incluída una nave espacial) puede orbitar a su alrededor exactamente igual que en torno a un astro, a pesar de que en ellos no haya ningún cuerpo con masa.

¿Y todo esto a qué viene? Pues viene a que aprovechando la interacción gravitatoria entre los distintos astros, y circulando a través de los puntos de Lagrange, se configura una especie de red de metro interplanetaria de mínima energía que nos permite viajar entre los distintos planetas y lunas con un coste energético mucho menor que en las órbitas de transferencia de Hohmann-Vetchinkin. De hecho, con un coste energético próximo a cero. Este metro, con sus estaciones en los puntos de Lagrange de los diversos pares de astros, se conoce como la red de transporte interplanetario.
El metro interplanetario. 

Esquema conceptual de la red de transporte interplanetario. NASA

La red de transporte interplanetario (ITN, por sus siglas en inglés) es un conjunto de rutas cósmicas que requieren muy poca y a menudo ninguna propulsión para que una nave espacial las recorra. Teóricamente, la energía de impulsión necesaria una vez iniciado el viaje podría ser cero; en la práctica, estaría muy próxima a cero. Esto fue demostrado por el ICE internacional en 1978 y la sonda lunar japonesa Hiten en 1991; después, ha sido utilizado por otras naves espaciales como la Génesis norteamericana (2001) o la SMART-1 de la Agencia Espacial Europea (2003).

Trayectoria descrita en la realidad por la nave espacial Génesis, utilizando el concepto de red de transporte interplanetario (2001-2004). Imagen: NASA.

Una trayectoria ITN de entrada al sistema solar interior con coste energético mínimo, vía los lagrangianos L1 y L2 del sistema Sol-Júpiter. Imagen: R. A. Tacchi en Interplanetary Transport Network, Universidad de California en Davis

Toda la propulsión necesaria para la realización de un viaje así se aplica durante el lanzamiento, con el propósito de alejar la nave del planeta Tierra y colocarla en un rumbo determinado a una velocidad precisa. A partir de ese punto, todo sucede solo, sin necesidad de aportar ninguna otra energía de impulsión más que para las posibles correcciones. Eso sí, el rumbo y la velocidad han de ser exactas de narices, pero esto es algo que ya cae actualmente dentro de las posibilidades tecnológicas humanas. De esta manera, toda la energía necesaria para el viaje se obtiene mediante la interacción gravitatoria con los distintos astros a través de sus puntos de Lagrange. Aplicando esta técnica no se requieren grandes motores ni grandes cargas de combustible (una vez ya estás en el espacio), sino sólo lo imprescindible para maniobrar en caso necesario.

La posibilidad de este metro interplanetario de consumo casi-cero ya fue teorizada por el matemático Henri Poincaré a finales del siglo XIX, pero no se pudo demostrar en la práctica hasta los vuelos de la ICE en 1978 y la Hiten en 1991. A partir de ahí se realizó un importantísimo trabajo de matemática aplicada, conocido en todo el mundo menos aquí (como siempre), por Gerard Gómez de la Universitat de Barcelona y Josep Masdemont de la Universitat Politècnica de Catalunya; sobre esta base, Martin Lo de la Universidad Purdue desarrolló una herramienta computacional llamada LTool, que permite calcular estas trayectorias y viene siendo utilizada desde entonces por el Jet Propulsion Laboratory y otras instituciones astronáuticas para crear el trazado de la red.

El principal problema con estas trayectorias es que son típicamente más largas que las órbitas de escape y las órbitas de transferencia de Hohmann-Vetchinkin, y además el paso por los puntos de Lagrange puede llegar a ser exasperantemente lento si queremos mantenernos en el coste energético mínimo. Por otra parte, las ventanas de lanzamiento óptimas pueden llegar a hallarse muy separadas entre sí. Esto tiene soluciones mixtas posibles, que con poco aporte de energía adicional pueden mejorar bastante algunos de los peores cuellos de botella, pero aún así la red de transporte interplanetario sólo resulta verdaderamente interesante cuando el tiempo de viaje es secundario. Por ello, en la actualidad sólo se plantea para sondas automáticas, no para vuelos tripulados. Pero esto podría cambiar en cualquier momento, y de hecho ya hay varias propuestas que utilizarían la ITN para misiones tripuladas.

La "cola" de la galaxia Renacuajo son los restos de uno de estos túneles de baja energía que quedó establecido en el pasado, cuando otra galaxia pasó cerca, por donde se deslizaron las estrellas de una a otra.

La comprensión cada vez mejor del problema de los tres cuerpos y de las dinámicas asociadas a los puntos de Lagrange no sólo son de interés en la exploración espacial. Esta idea de los pasadizos de baja energía tiene otras aplicaciones. Por ejemplo: en el año 2000 Charles Jaffé, un químico de la Universidad de Virginia Occidental, observó que bajo determinadas condiciones experimentales las rutas que toman los electrones de valencia en átomos de Rydberg son muy parecidas a la trayectoria de la sonda Génesis. Y cuando estos átomos se someten a campos eléctricos y magnéticos perpendiculares, también realizan estos recorridos tubulares. Esto ha sentado las bases para el desarrollo futuro de nuevas teorías y aplicaciones en química y tecnologías de materiales, pues las matemáticas subyacentes son válidas a todas las escalas, desde los átomos a las distancias intergalácticas.

Hablando de galaxias, científicos de las universidades de Tokio y Edimburgo han mostrado que unos tubos relacionados con los puntos de Lagrange conducen a la “evaporación” de pequeños cúmulos estelares en órbita alrededor de algunas galaxias. Este efecto es mucho más notable cuando interaccionan dos de ellas: la galaxia Renacuajo manifiesta evidencias de un episodio muy violento en su pasado, un raspón como si dijéramos. La enorme cola que se extiende tras el renacuajo señala el lugar donde miles de estrellas entraron en tubos conectados con otra galaxia que pasó cerca. La cola del renacuajo es, pues, un puente hacia la nada de 280.000 años-luz. Otras galaxias presentan túneles de interconexión similares.

Aúnque aún no se han elaborado los mapas, cabe esperar que existan trayectorias parecidas conectando las estrellas entre sí; por ejemplo, al Sol con las estrellas cercanas. Esto constituiría una red de transporte interestelar donde una nave del tipo de las Voyager podría viajar directamente a Alfa Centauri, por decir algo, sin coste de propulsión adicional alguno. Le costaría miles de años hacerlo, pero aquí asoma un asunto interesante: en el pasado, hubo estrellas que estaban mucho más cerca del Sol (y en el futuro volverá a haberlas). Es posible que nos intercambiáramos material con ellas a través de estos canales. Qué material exactamente queda por el momento a la imaginación de cada cual.

Hace apenas cuarenta años y una semana, Venera 7 se posaba con bien en Venus tras utilizar una primitiva órbita de transferencia Hohmann-Vetchinkin con un coste energético de 3,8 megajulios por kilo. Fue una hazaña extraordinaria, ejecutada con tecnologías primitivas y a lo bruto porque en ese momento no se podía hacer de ninguna otra manera. Ahora sabemos que es posible llegar a la mayor parte de sitios interesantes en el sistema solar, y quizás en torno a otras estrellas y galaxias, con una milésima parte de esa energía. Si no lo estamos haciendo ya más y mejor, no es porque no sepamos, sino por simple ceguera y mezquindad. Ah, sí, por cierto. En salvar a los bancos, europeos y norteamericanos hemos comprometido dinero suficiente (unos trece billones de dólares sólo en los EEUU) para hacer unas mil misiones tripuladas a Marte y mantener el CERN durante más de diez mil años: las dos cosas a la vez y pagadas a tocateja con un solo cheque. Menos mal que no había pasta, ¿eh?

Para más información:

• Ross, Shane D (2006), The interplanetary transport network, en American Scientist, vol. 94, págs. 230-237.
• Conley, C. C. (1968), Low energy transit orbits in the restricted three-body problem. En SIAM Journal on Applied Mathematics 16:732–746.
• Fukushige, T., y D. C. Heggie (2000), The time-scale of escape from star clusters. En Monthly Notices of the Royal Astronomical Society 318:753–761.
• Jaffé, C., S. Ross, M. Lo, J. Marsden, D. Farrelly y T. Uzer (2002), Statistical theory of asteroid escape rates. En Physical Review Letters 89:011101.
• Marsden, J. E., y S. D. Ross. (2006), New methods in celestial mechanics and mission design, en Bulletin of the American Mathematical Society 43:43–73.
• Smith, D. L. (2002), Next exit 0.5 million kilometers, en Engineering & Science LXV(4):6–15.

La posible muerte de los diagramas de Feynman y el nacimiento de una nueva era en física de partículas teórica.

Fuente: Francis (th)e mule

Trabajos recientes de Juan Maldacena y Nima Arkani-Hamed parecen apuntar a que la física teórica de partículas elementales está entrando en una nueva era en la que se prescindirá de los diagramas de Feynman. Quizás no lo sabes, pero un físico de partículas teórico es una calculadora humana de diagramas de Feynman. No es difícil hacer los cálculos, pero hay que armarse de paciencia y no se pueden cometer errores. Evaluar unos cientos de diagramas de Feynman para obtener una aproximación al orden más bajo (LO por Leading-Order) requiere evaluar unas decenas de miles de integrales, para muchos procesos en cromodinámica cuántica (QCD). Obtener las correcciones superiores, NLO (Next-to-Leading-Order) y NNLO (Next-to-Next-to-Leading-Order), requiere la evaluación de decenas de miles de diagramas de Feynman. Decenas de miles de diagramas para obtener correcciones del orden del 3% o incluso menores, pero necesarias para verificar la ausencia de nueva física en las colisiones del LHC en el CERN y del Tevatrón en el Fermilab. Sin la ayuda de ordenadores evaluar correcciones NNLO es una tarea imposible. Pero incluso con su ayuda es una labor ardua y propensa a errores. La física de partículas necesita entrar en una nueva era y Juan Maldacena, Nima Arkani-Hamed y el mismísimo Edward Witten están liderando el camino hacia ella. Nos lo cuenta Neil Turok, “Particle physics: Beyond Feynman’s diagrams,” Nature 469: 165–166, 13 January 2011.

La matemática de la física de partículas elementales es conocida como teoría cuántica de campos. Esta teoría describe como se propagan los campos cuánticos que describen las partículas, como colisionan e interaccionan entre sí, como se producen nuevas partículas, etc. Todos los procesos que se observan en los grandes aceleradores de partículas (como el Tevatrón y el LHC). Las técnicas matemáticas utilizadas se basan en un desarrollo en serie de potencias denominado análisis perturbativo. La herramienta básica para desarrollar este trabajo son los diagramas que introdujo el genial físico americano Richard Feynman. Sus diagramas representan integrales múltiples complicadas de una forma que permite minimizar los errores a la hora de escribir dicha integral. Sin embargo, estos diagramas sirven de poco a la hora de evaluar estas integrales. Muchos físicos teóricos pasan la mayor parte de su vida evaluando diagramas de Feynman. Las reglas de dibujo de estos diagramas garantizan el cumplimiento de las leyes de la relatividad especial (el principio de localidad) y de las leyes de probabilidad de la mecánica cuántica (el principio de unitariedad). Por ello, estos diagramas son muy redundantes y en muchos cálculos que requieren cientos de páginas repletas de integrales, al final del cálculo la mayoría de los términos se compensa mutuamente, desaparece y queda un resultado final muy sencillo que se puede escribir en una línea (muy al gusto de cualquier físico de partículas experimental). Muchos físicos teóricos han buscado técnicas que simplifiquen la evaluación de estos resultados finales evitando el uso de diagramas de Feynman, pero pocos han tenido éxito, … hasta ahora.

En 1985, dos físicos de partículas del Fermilab, Stephen J. Parke y T. R. Taylor, decidieron calcular los diagramas de Feynman de uno de los procesos más sencillos en cromodinámica cuántica: la colisión de dos gluones que produce como resultado cuatro gluones (os recuerdo que los gluones son las partículas responsables de que los quarks estén confinados dentro del protón y del neutrón; son como el “pegamento” que los une). Este proceso de fusión de gluones es muy habitual en el LHC del CERN, un acelerador donde las colisiones gluón-gluón son mucho más numerosas que las colisiones quark-quark y gluón-quark. El término dominante de este proceso con 6 gluones (LO) requería evaluar 220 diagramas de Feynman, es decir, decenas de miles de integrales matemáticas. Pero Parke y Taylon encontraron que el resultado final se simplificaba si se aplicaban unas nuevas reglas muy sencillas. Era la primera señal de que los diagramas de Feynman quizás estaban complicando las cosas en lugar de facilitarlas. El artículo técnico de solo una página y media es Stephen J. Parke and T. R. Taylor, “Amplitude for n-Gluon Scattering,” Phys. Rev. Lett. 56: 2459–2460, 1986. Parke y Taylor retaron a los físicos teóricos de cuerdas a demostrar de forma rigurosa sus nuevas reglas (“we challenge the string theorists to prove more rigorously that our equation is correct“). Y los teóricos de cuerdas y especialistas en supergravedad recogieron el guante y encontraron la razón por la cual dichas reglas ”gluodinámicas” funcionaban. Y algunos físicos, como Bern, Dixon y Kosower, de Britto, Cachazo y Feng, y de Britto, Cachazo, Feng y Witten, se dedicaron a desarrollar nuevas técnicas aún más poderosas (y sin usar diagramas de Feynman).

Pero no ha sido hasta 2010 cuando estas nuevas técnicas han empezado a brillar con luz propia. Los responsables son dos artículos recientes en ArXiv de Luis F. Alday, Davide Gaiotto, Juan Maldacena, Amit Sever y Pedro Vieira (julio de 2010), y de Nima Arkani-Hamed, Jacob L. Bourjaily, Freddy Cachazo, Simon Caron-Huot y Jaroslav Trnka (diciembre de 2010). Arkani-Hamed y sus colegas utilizan herramientas de la teoría de los twistors, desarrollada por Roger Penrose en los 1970 y reivindicada por los teóricos de cuerdas de la mano de Ed Witten en 2004, y de geometría algebraica para calcular procesos de interacción muy complejos en el régimen de acoplamiento débil. Juan Maldacena y sus colegas utilizan relaciones no locales entre unas magnitudes llamadas bucles de Wilson que surgen gracias a la matemática de la integrabilidad cuántica en el régimen de acoplamiento fuerte. Dos trabajos que se complementan, pues estudian límites opuestas en la misma teoría. Dos trabajos que nos muestran en física de partículas hay más cosas que calcular diagramas de Feynman. Quizás estamos asistiendo a una nueva revolución en ciernes en la física de partículas elementales teórica.

Quizás estas nuevas técnicas matemáticas sugerirán nuevos principios físicos que guíen el desarrollo de las teorías físicas más allá del modelo estándar. Habrá que estar atentos a estos progresos.

Más información en inglés en “Twistors killed the Feynman diagram,” Francis’ world inside out, January 12, 2011.

300 cursos online gratis de las mejores universidades (en inglés).

En http://www.openculture.com/freeonlinecourses tenemos casi 300 cursos de ciencias y artes. También se incluye un enlace a cursos de idiomas. También recomiendo http://academicearth.org/ como fuente de cursos en vídeo.
Y ya que estamos:
http://www.youtube.com/user/StanfordUniversity
http://www.youtube.com/user/UCBerkeley

Obsolescencia programada

Descubren antimateria encima de tormentas eléctricas

Fuente: ALT1040

 Por Alan Lazalde el 11 de Enero de 2011 en Ciencia.

Con la ayuda del telescopio espacial de rayos gamma Fermi, científicos descubrieron lo impensable: rayos de antimateria producidos encima de tormentas eléctricas. Se confirmó que el fenómeno, nunca antes visto por cierto, es causado por ráfagas de rayos gamma terrestres (TGF) generadas al interior de las tormentas eléctricas y asociados directamente con los relámpagos.



El descubrimiento fue anunciado ayer por Michael Briggs durante un encuentro de la American Astronomical Society. El científico mencionó que

esas señales son la primera evidencia de que las tormentas eléctricas crean rayos de partículas de antimateria

Son tres los pasos que llevan a la creación y detección de la antimateria producida por las tormentas:

1. Campos eléctricos encima de las tormentas crean una avalancha de electrones con dirección al cielo. Cuando estos se estrellan contra las moléculas en el aire, se emiten rayos gamma —los de mayor energía.
2. La energía de los rayos gamma acelera los electrones a una velocidad cercana a la de la luz. Pero cuando algún rayo pasa cerca del núcleo de un átomo, el rayo gamma se transforma en un par de partículas: el electrón y su antipartícula, el positrón.
3. Hasta aquí el TGF ha tenido una duración de 1.98 milisegundos, tiempo suficiente para que alcance la altitud necesaria para ser interceptado por el telescopio Fermi, quien no hace sino confirmar la presencia de una aniquilación partícula-antipartícula.

De izquierda a derecha:

Se estima que todos los días ocurren unos 500 TGF en nuestro planeta, aunque pocos son detectados, y de hecho se piensa que todos ellos emiten rayos electrón/positrón.

Estoy seguro para la mayoría de nosotros esto ha sido una sorpresa, de esas que sólo un descubrimiento científico nos puede dar.

Imagen e información: NASA

Kinect + realidad virtual + Hatsune Miku = Epic Win

Fuente: alt1040.com

En efecto, han creado una nueva forma de marioneta uniendo el Kinect a un modelo en 3D de Hatsune Miku.