jueves, 26 de julio de 2012
Un medio transparente a un solo fotón y opaco a un haz con muchos fotones
Los medios ópticos no lineales permiten lograr una interacción fuerte entre fotones que puede amplificar fenómenos muy débiles con aplicaciones prácticas (potenciales) muy interesantes. Peyronel et al. publican en Nature un nuevo material en el que los fotones individuales se propagan libremente, pero interaccionan tan fuertemente entre sí que si dos fotones se encuentran presentes en dicho medio uno de ellos es absorbido rápidamente. Como resultado, este medio óptico no lineal permite desarrollar dispositivos tan interesantes como conmutadores ópticos para un solo fotón, o puertas lógicas cuánticas basadas en fotones individuales. Nos lo cuenta Thad G. Walker, “Quantum optics: Strongly interacting photons,” Nature, Published online 25 July 2012, que se hace eco del artículo técnico de Thibault Peyronel et al., “Quantum nonlinear optics with single photons enabled by strongly interacting atoms,” Nature, Published online 25 July 2012. La formulación matemática de un modelo del nuevo medio no lineal aparece en la información suplementaria del artículo.
La teoría cuántica del campo electromagnético (desarrollada en 1926 por Max Born, Pascual Jordan y Werner Heisenberg) describe dicho campo como compuesto de partículas llamadas fotones (excitaciones cuánticas del campo electromagnético con una energía “cuantizada” igual a hν, donde h es la constante de Planck y ν es la frecuencia de la luz). Los fotones interaccionan entre sí muy débilmente, aunque lo hacen fuertemente con las partículas cargadas (como electrones y núcleos atómicos). La mayoría de los materiales presentan una respuesta óptica lineal (un haz de muchos fotones se dispersa como si cada uno de ellos se moviera sin que existieran los demás). Sin embargo, hay materiales que presentan una respuesta óptica no lineal, en los que un haz de luz muy intenso conlleva una interacción fuerte entre los propios fotones del haz. Peyronel et al . han dirigido un haz de fotones en gas atómico en un estado de superposición que permite que los fotones individuales se transformen en polaritones de Rydberg (un tipo de excitación colectiva que agrupa el estado de múltiples átomos y un solo fotón). Estos polaritones tienen la propiedad de que son opacos a otros fotones y los abserben muy fuertemente. A la salida del gas atómico, los polaritones se transforman de nuevo en un único fotón, con lo que éste actúa como un transformador de haces de fotones en fotones individuales.
Los átomos del gas tienen tres niveles de energía: el estado fundamental |g> (con un nivel de energía Eg), un estado excitado |r> (con energía Er) y un estado intermedio |e> (con energía Ee). Los fotones de frecuencia ν1 que se dirigen al gas atómico y que obedecen la ecuación de Bohr, h ν1 = Ee - Eg, son absorbidos salvo cuando incide la luz de un láser con frecuencia ν2 que cumple la condición h (ν1+ν2) = Er - Eg. Este fenómeno se llama transparencia inducida electromagnéticamente (IET) y excita de forma colectiva a los átomos del gas y al fotón en un estado llamado polaritón. Los fotones que obedcen la condición de IET se transmiten como polaritones con alta probabilidad, mientras que aquellos que la violan son absorbidos. Como resultado se ha fabricado un conmutador (o interruptor) controlado de forma completamente óptica. El diseño del gas óptico utilizado por Peyronel y sus colegas permite asegurar que un solo polaritón de Rydberg se encuentra en el medio al mismo tiempo (con una probabilidad superior al 91% de los casos). En aplicaciones prácticas interesa que esta probabilidad sea lo más cercana posible al 100%, por lo que en un futuro habrá que mejorar su diseño. Aún así, el futuro es muy prometedor para este tipo de sistemas.
lunes, 23 de julio de 2012
¿Por qué la Tierra es tan seca?
Fuente: Ciencia Kanija
Un nuevo análisis del modelo común de disco de acreción, que explica cómo se formaron los planetas en un disco de escombros alrededor del Sol, descubrió una posible razón para la comparativa sequedad de la Tierra. Liderado por Rebecca Martin y Mario Livio del Instituto Científico del Telescopio Espacial en Baltimore, Maryland, el estudio encontró que nuestro planeta se formó a partir de escombros rocosos en una región más caliente y seca, dentro de lo que se conoce como “línea de nieve”. La línea de nieve en nuestro Sistema Solar actualmente se encuentra en el centro del cinturón de asteroides, una reserva de material entre Marte y Júpiter; más allá de este punto, la luz del Sol es demasiado débil para fundir los helados escombros dejados por el disco protoplanetario. Los anteriores modelos de discos de acreción sugerían que la línea de nieve se encontraba mucho más cerca del Sol hace 4500 millones de años, cuando se formó la Tierra.
Fecha Original: 17 de julio de 2012
Enlace Original
Artículo publicado el 17 de julio de 2012 en HubbleSite
Con largas extensiones de océanos, ríos
que serpentean a lo largo de cientos de kilómetros y descomunales
glaciares cerca de los polos norte y sur, la Tierra no parece tener
escasez de agua. Y aun así menos de un uno por ciento de la masa de
nuestro planeta se encuentra en el agua, e incluso esta puede haber sido
transportada por cometas y asteroides tras la formación inicial de la
Tierra.
Los astrónomos están desconcertados por
esta carencia de agua en la Tierra. El modelo estándar que explica cómo
se formó el Sistema Solar a partir de un disco protoplanetario, un disco
giratorio de gas y polvo que rodeaba nuestro Sol hace miles de millones
de años, sugiere que nuestro planeta debería ser un mundo acuoso. La
Tierra debería haberse formado a partir de material helado en una zona
alrededor del Sol donde las temperaturas fuesen lo bastante frías para
que el hielo se condensase a partir del disco. Por tanto, la Tierra
debería haberse formado a partir de material rico en agua. Entonces,
¿por qué nuestro planeta es comparativamente tan seco?
Un nuevo análisis del modelo común de disco de acreción, que explica cómo se formaron los planetas en un disco de escombros alrededor del Sol, descubrió una posible razón para la comparativa sequedad de la Tierra. Liderado por Rebecca Martin y Mario Livio del Instituto Científico del Telescopio Espacial en Baltimore, Maryland, el estudio encontró que nuestro planeta se formó a partir de escombros rocosos en una región más caliente y seca, dentro de lo que se conoce como “línea de nieve”. La línea de nieve en nuestro Sistema Solar actualmente se encuentra en el centro del cinturón de asteroides, una reserva de material entre Marte y Júpiter; más allá de este punto, la luz del Sol es demasiado débil para fundir los helados escombros dejados por el disco protoplanetario. Los anteriores modelos de discos de acreción sugerían que la línea de nieve se encontraba mucho más cerca del Sol hace 4500 millones de años, cuando se formó la Tierra.
“Al contrario que en el modelo estándar
de disco de acreción, la línea de nieve en nuestro análisis nunca migra
dentro de la órbita de la Tierra”, dice Livio. “En lugar de esto,
permanece más lejos de la órbita de la Tierra, lo que explica por qué
nuestra Tierra es un planeta seco. De hecho, nuestro modelo predice que
los otros planetas interiores, Mercurio, Venus, y Marte, también son
relativamente secos”.
Los resultados se han aceptado para su publicación en la revista Monthly Notices of the Royal Astronomical Society.
En el modelo convencional, el disco
protoplanetario alrededor del Sol está completamente ionizado (un
proceso en el cual los electrones son arrancados de los átomos) y
canaliza materia sobre nuestra estrella, que calienta el disco. La línea
de nieve inicialmente está lejos de la estrella, tal vez al menos a
1600 millones de kilómetros. Con el tiempo el disco agota su material,
se enfría y arrastra hacia el interior a la línea de nieve, más allá de
la órbita de la Tierra, antes de que pase suficiente tiempo para que se
forma nuestro planeta.
“Si la línea de nieve estaba dentro de
la órbita de la Tierra cuando se formó nuestro planeta, entonces debería
haber sido un cuerpo helado”, explica Martin. “Planetas como Urano y
Neptuno se formaron más allá de la línea de nieve y están compuestos por
decenas de puntos porcentuales de agua. Pero la Tierra no tiene mucha
agua, y eso siempre ha sido un misterio”.
El estudio de Martin y Livio encontró un
problema con el actual modelo de disco de acreción para la evolución de
la línea de nieve. “Dijimos, espera un momento, los discos alrededor de
las estrellas jóvenes no están completamente ionizados”, señala Livio.
“No son discos estándar debido a que no hay suficiente calor y radiación
para ionizar el disco”.
“Los objetos muy calientes, como enanas
blancas y fuentes de rayos-X, liberan la suficiente energía para ionizar
sus discos de acreción”, añade Martin. “Pero las estrellas jóvenes no
tienen suficiente radiación o material incidente para proporcionar el
suficiente impulso energético para ionizar los discos”.
Por tanto, si los discos no están
ionizados, no hay mecanismos que puedan permitir el flujo el materia a
través de la región y que caiga en la estrella. En su lugar, el gas y el
polvo orbitan a la estrella sin moverse hacia dentro, creando lo que se
conoce como “zona muerta” en el disco. La zona muerte se extiende
normalmente desde aproximadamente 0,1 unidades astronómicas a unas pocas
unidades astronómicas más allá de la estrella. (Una unidad astronómica
es la distancia entre la Tierra y el Sol, unos 150 millones de
kilómetros). Esta zona actúa como un tapón, evitando que la materia
emigre hacia la estrella. El material, no obstante, se apila en la zona
muerte e incrementa su densidad, de la misma forma que la gente se
agolpa alrededor de la entrada de un concierto esperando la apertura de
las puertas.
La densa materia empieza a calentarse
debido a la compresión gravitatoria. Este proceso, a su vez, calienta el
área fuera del tapón, evaporando el material helado y convirtiéndolo en
material seco. La Tierra se formó en esta región más caliente, la cual
se extiende unas pocas unidades astronómicas alrededor del Sol, a partir
de material seco. La versión modificada de Martin y Livio del modelo
estándar explica por qué la Tierra no terminó con una abundancia de
agua.
Martin advierte que el modelo revisado
no es un borrador de cómo se comportan todos los discos alrededor de
estrellas jóvenes. “Las condiciones dentro del disco variarán de una
estrella a otra”, dice Livio, “y el azar, sobre todo, determinó los
resultados precisos para nuestra Tierra”.
Fecha Original: 17 de julio de 2012
Enlace Original
viernes, 20 de julio de 2012
Las matemáticas del bosón de Higgs, para las abuelas cansadas de cháchara (Parte I)
Fuente: Francis (th)E mule
Igor Campillo, físico y Director de Euskampus en la Universidad del País Vasco, Campus de Excelencia Internacional, lo ha dejado más claro que el agua en “La partícula que tu abuela nunca entenderá por mucho que se lo expliques,” Amazings.es, 17 julio 2012. “Me temo que todo este esfuerzo resulta vano desde el punto de vista conceptual, al menos si se aspira a explicar el bosón de Higgs “hasta a mi abuela”… “Comprender es acostumbrarse.” Según aprendemos, lo que nos había parecido inescrutable al principio resulta ser trivial, simplemente por el hecho de trabajar en ello. Por eso resulta tan difícil captar lo que es la mecánica cuántica, porque está fuera de nuestra experiencia cotidiana y uno no se puede acostumbrar a ella utilizando ejemplos de nuestro día a día. Sólo tras mucho operar y calcular, se empiezan a captar sutilezas, conceptos e implicaciones que de otra forma son inimaginables. Entender y explicar el bosón de Higgs sólo puede hacerse dentro del formalismo donde aparece. No podemos hacer “un como si”. No admite traducción e interpretación simultánea.”
¿Qué es el bosón de Higgs? La partícula con la que se puede observar el campo de Higgs. ¿Qué es el campo de Higgs? Un campo con el que interaccionan las partículas que tienen masa. Esta interacción es cuántica, pero podemos hacernos una idea de cómo funciona utilizando la teoría clásica de campos. Nos lo cuenta The Unapologetic Mathematician en “The Higgs Mechanism part 1: Lagrangians,” July 16, “The Higgs Mechanism part 2: Examples of Lagrangian Field Equations,” July 17, “The Higgs Mechanism part 3: Gauge Symmetries,” July 18, y “The Higgs Mechanism part 4: Symmetry Breaking,” July 19. Recomiendo una lectura a estas entradas.
He pensado en traducir dichas entradas, pero no tengo tiempo y ya hice algo parecido hace algún tiempo (abril de 1999). Quizás conviene recordarlo.

La rotura espontánea de la simetría fue descubierta por Heisenberg en 1932 en su estudio de los materiales ferromagnéticos, y aplicada por Nambu y Goldstone, a principios de los 1960, a teorías de campos en física de la materia condensada (teorías de aforo (gauge) global). En 1964, Higgs (y otros autores) la aplicó a teorías de aforo local descubriendo un mecanismo para la generación de la masa de las partículas elementales. Dicho mecanismo está en la base de la teoría electrodébil, desarrollada por Glashow, Weinberg y Salam, premios Nobel de Física en 1979. La teoría electrodébil es una teoría de aforo local que unifica la fuerza electromagnética mediada por el fotón, que
no tiene masa, y la fuerza débil mediada por los bosones vectoriales
intermedios
que unifica la fuerza electromagnética mediada por el fotón, que
no tiene masa, y la fuerza débil mediada por los bosones vectoriales
intermedios 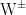 y
y  ,
que tienen masa no nula. En esta teoría, se produce una rotura
espontánea de la simetría mediante el mecanismo de Higgs, por el cual
los bosones vectoriales adquieren masa y queda como remanente una
partícula masiva, el bosón escalar de Higgs, que ha sido
encontrado experimentalmente el pasado 4 de julio de 2012.
,
que tienen masa no nula. En esta teoría, se produce una rotura
espontánea de la simetría mediante el mecanismo de Higgs, por el cual
los bosones vectoriales adquieren masa y queda como remanente una
partícula masiva, el bosón escalar de Higgs, que ha sido
encontrado experimentalmente el pasado 4 de julio de 2012.
‘t Hooft probó en su tesis doctoral, dirigida por Veltman, que una teoría de aforo local con rotura espontánea de la simetría, como la teoría electrodébil, es renormalizable. De esta forma se definió un procedimiento consistente para realizar cálculos de gran precisión en esta teoría y, entre ellos, la predicción de las masas de las partículas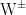 y
y  , descubiertas en el CERN en 1983, y del quark t (top), descubierto en el Fermilab en 1995.
, descubiertas en el CERN en 1983, y del quark t (top), descubierto en el Fermilab en 1995.
En este artículo se estudiará la generación de masa mediante rotura espontánea de la simetría utilizando una teoría clásica de campos. Primero, repasaremos brevemente la notación tensorial (de índices) para vectores y covectores, la relatividad especial, la diferencia entre vectores axiales y polares, y la formulación covariante o relativista de las ecuaciones de Maxwell. Seguidamente, repasaremos la formulación lagrangiana de campos clásicos y su aplicación a un campo escalar cargado (complejo) que tiene simetría de aforo global de tipo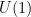 .
Imponiendo la invarianza de las ecuaciones de este campo ante
transformaciones de aforo locales se obtiene un campo electromagnético.
Finalmente, estudiaremos la aplicación de la rotura de simetría al campo
escalar cargado con simetría de aforo global, el mecanismo de
Goldstone, y con simetría de aforo local, el mecanismo de Higgs, que
permite al campo electromagnético adquirir masa “tragándose” una de las
componentes del campo escalar y dejando como remanente a la otra, el
bosón de Higgs.
.
Imponiendo la invarianza de las ecuaciones de este campo ante
transformaciones de aforo locales se obtiene un campo electromagnético.
Finalmente, estudiaremos la aplicación de la rotura de simetría al campo
escalar cargado con simetría de aforo global, el mecanismo de
Goldstone, y con simetría de aforo local, el mecanismo de Higgs, que
permite al campo electromagnético adquirir masa “tragándose” una de las
componentes del campo escalar y dejando como remanente a la otra, el
bosón de Higgs.
 en el espacio vectorial
en el espacio vectorial 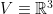 , con componentes
, con componentes  y
y 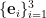 una base de dicho espacio vectorial. Entonces, se puede expresar
una base de dicho espacio vectorial. Entonces, se puede expresar  en coordenadas como
en coordenadas como
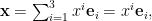
donde en la última expresión hemos usado el convenio de suma de índices repetidos de Einstein, según el cual los términos (productos) con índices repetidos representan la suma de dichos términos respecto a dichos índices.
Se denomina espacio vectorial dual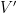 al espacio de formas lineales (covectores) en
al espacio de formas lineales (covectores) en 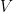 . Un covector
. Un covector  es una función lineal
es una función lineal 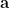 que transforma un vector
que transforma un vector 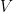 en un número
en un número 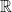 , es decir, tal que
, es decir, tal que

donde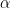 y
y 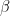 son números (escalares). En función de las coordenadas de
son números (escalares). En función de las coordenadas de  podemos escribir
podemos escribir  como
como 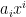 (recuerda que esto significa
(recuerda que esto significa 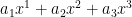 ); gracias a la linealidad
); gracias a la linealidad 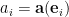 .
.
Asociada a la base de vectores , podemos elegir covectores
, podemos elegir covectores  que cumplan
que cumplan
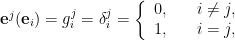
donde es la delta de Krocneker. Estos covectores cumplen que
es la delta de Krocneker. Estos covectores cumplen que  , y se comprueba que forman una base de
, y se comprueba que forman una base de 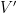 , lo que permite escribir
, lo que permite escribir  , ya que
, ya que

donde hemos usado que los índices son mudos. La dimensión de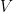 es igual a la dimensión de
es igual a la dimensión de 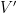 y, por tanto, son espacios vectoriales isomorfos, luego podemos considerar un vector
y, por tanto, son espacios vectoriales isomorfos, luego podemos considerar un vector 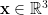 tanto como vector
tanto como vector  o como covector
o como covector 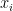 . A los vectores y covectores también se les denomina vectores contravariantes
. A los vectores y covectores también se les denomina vectores contravariantes  y covariantes
y covariantes 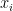 , respectivamente. Para subir y bajar índices se usa el tensor fundamental
, respectivamente. Para subir y bajar índices se usa el tensor fundamental  , actuando de la forma
, actuando de la forma

El espacio-tiempo euclídeo es el espacio invariante ante transformaciones de
es el espacio invariante ante transformaciones de
Galileo, que son las que dejan invariante el tiempo y la distancia euclídea en el espacio, definida mediante el producto escalar euclídeo

Como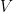 y
y 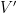 son isomorfos, se puede definir el producto escalar como un producto interior
son isomorfos, se puede definir el producto escalar como un producto interior
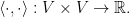
Para distancias infinitesimales obtenemos la condición

 )
y usa el espacio-tiempo de Minkowski que es invariante ante
trasformaciones de Lorentz, que son las que preservan la métrica
pseudo-euclídea
)
y usa el espacio-tiempo de Minkowski que es invariante ante
trasformaciones de Lorentz, que son las que preservan la métrica
pseudo-euclídea
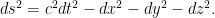
Al contrario que en el espacio-tiempo euclídeo, los vectores contravariantes y los covariantes en el espacio de Minkowski tienen componentes que difieren (aunque solo en su signo), en concreto,
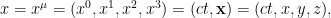

respectivamente. Introduciendo el tensor métrico fundamental
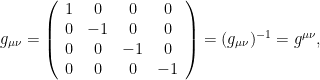
podemos escribir la métrica como

Se definen los operadores diferenciales


que conducen al operador de segundo orden

de d’Alembert, que es invariante Lorentz.
 se denomina axial (pseudovector) o polar (vector) en función de si
cambia o no, respectivamente, de signo cuando se realiza una reflexión
espacial,
se denomina axial (pseudovector) o polar (vector) en función de si
cambia o no, respectivamente, de signo cuando se realiza una reflexión
espacial,  . La importancia de esta diferencia se debe a que el producto vectorial de dos vectores polares
. La importancia de esta diferencia se debe a que el producto vectorial de dos vectores polares 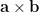 es un vector axial.
es un vector axial.
Introduciendo el tensor completamente antisimétrico de rango 3 de Levi-Civita definido como
definido como
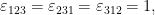


se escribe el producto vectorial en componentes como
en componentes como 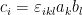 (recuerda que hay que sumar respecto a los índices repetidos, en este caso,
(recuerda que hay que sumar respecto a los índices repetidos, en este caso,  ).
).
Asociado al producto vectorial podemos escribir un tensor anti-simétrico de rango 2 de la forma que permite escribir (suma índices repetidos)
que permite escribir (suma índices repetidos)
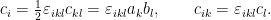
Así, para el rotacional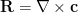 tenemos
tenemos
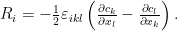
En general, todos los vectores axiales se pueden representar como tensores anti-simétricos de rango 2 de la forma
se pueden representar como tensores anti-simétricos de rango 2 de la forma  , con lo que podemos escribir
, con lo que podemos escribir 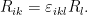
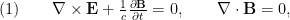
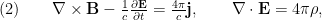
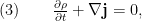
donde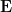 ,
, 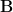 ,
,  ,
,  y
y  son el campo eléctrico, la intensidad de campo magnético, la densidad
de carga, la corriente de carga y la velocidad de la luz,
respectivamente. Las ecuaciones
son el campo eléctrico, la intensidad de campo magnético, la densidad
de carga, la corriente de carga y la velocidad de la luz,
respectivamente. Las ecuaciones 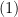 corresponden a la Ley de Faraday, un campo magnético variable genera un
campo eléctrico, y a la ausencia de cargas magnéticas (monopolos). Las
ecuaciones
corresponden a la Ley de Faraday, un campo magnético variable genera un
campo eléctrico, y a la ausencia de cargas magnéticas (monopolos). Las
ecuaciones  corresponden a la Ley de Ampère con el término añadido por Maxwell que
permite la generación de ondas electromagnéticas, y a la ley de Gauss,
la carga total en un volumen determina el campo en su superficie.
Finalmente, la ecuación
corresponden a la Ley de Ampère con el término añadido por Maxwell que
permite la generación de ondas electromagnéticas, y a la ley de Gauss,
la carga total en un volumen determina el campo en su superficie.
Finalmente, la ecuación  es la ley de conservación de la carga.
es la ley de conservación de la carga.
Las ecuaciones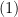 quedan automáticamente satisfechas si se introducen dos potenciales, uno escalar o eléctrico,
quedan automáticamente satisfechas si se introducen dos potenciales, uno escalar o eléctrico, 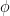 , y otro vectorial o magnético,
, y otro vectorial o magnético,  , de forma que
, de forma que
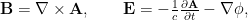
(ya que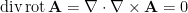 , y
, y 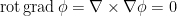 ).
).
En relatividad especial podemos definir un cuadrivector potencial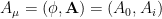 y los campos eléctrico y magnético se escriben
y los campos eléctrico y magnético se escriben


Definiendo el tensor covariante antisimétrico
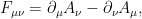
obtenemos que, de lo dicho anteriormente,


Definiendo un cuadritensor completamente antisimétrico de cuarto rango (igual a
(igual a 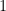 para permutaciones pares de
para permutaciones pares de  , a
, a 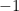 para permutaciones impares y a
para permutaciones impares y a 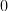 en otro caso), las ecuaciones
en otro caso), las ecuaciones 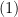 se pueden escribir como
se pueden escribir como

donde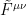 es el tensor dual de
es el tensor dual de 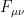 .
.
Introduciendo un cuadrivector corriente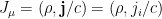 , podemos escribir las ecuaciones
, podemos escribir las ecuaciones  como
como
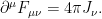
Además, se cumple automáticamente la ecuación de continuidad , ya que
, ya que

A partir del tensor del campo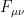 podemos definir dos invariantes
podemos definir dos invariantes

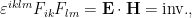
que indican que la energía se conserva y el campo electromagnético es transversal, respectivamente.
El campo electromagnético es invariante ante transformaciones de aforo (gauge) de tipo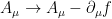 , donde
, donde  es una función escalar arbitraria, ya que
es una función escalar arbitraria, ya que 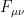 (los campos
(los campos 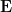 y
y  ) no cambian ante dicha transformación.
) no cambian ante dicha transformación.
 , mediante un principio de “mínima” acción: la acción
, mediante un principio de “mínima” acción: la acción
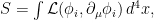
donde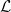 es la densidad lagrangiana, debe ser estacionaria
es la densidad lagrangiana, debe ser estacionaria  . Operando obtendremos las ecuaciones de Euler-Lagrange
. Operando obtendremos las ecuaciones de Euler-Lagrange
![\delta S=\int \left[\frac{\partial {\cal {L}}}{\partial \phi_i}\delta \phi_i + \frac{\partial {\cal {L}}}{\partial (\partial_\mu\phi_i)}\delta (\partial_\mu\phi_i)\right]\, d^4 x, \delta S=\int \left[\frac{\partial {\cal {L}}}{\partial \phi_i}\delta \phi_i + \frac{\partial {\cal {L}}}{\partial (\partial_\mu\phi_i)}\delta (\partial_\mu\phi_i)\right]\, d^4 x,](http://s0.wp.com/latex.php?latex=%5Cdelta+S%3D%5Cint+%5Cleft%5B%5Cfrac%7B%5Cpartial+%7B%5Ccal+%7BL%7D%7D%7D%7B%5Cpartial+%5Cphi_i%7D%5Cdelta+%5Cphi_i+%2B+%5Cfrac%7B%5Cpartial+%7B%5Ccal+%7BL%7D%7D%7D%7B%5Cpartial+%28%5Cpartial_%5Cmu%5Cphi_i%29%7D%5Cdelta+%28%5Cpartial_%5Cmu%5Cphi_i%29%5Cright%5D%5C%2C+d%5E4+x%2C&bg=ffffff&fg=000000&s=0)
e integrando por partes usando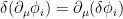 y que
y que 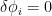 en el contorno, obtenemos
en el contorno, obtenemos
![\delta S=\int \left[ \frac{\partial {\cal {L}}}{\partial \phi_i} - \frac{\partial }{\partial x^\mu} \left(\frac{\partial {\cal {L}}}{\partial (\partial_\mu\phi_i)} \right)\right]\,\delta \phi_i\, d^4 x = 0, \delta S=\int \left[ \frac{\partial {\cal {L}}}{\partial \phi_i} - \frac{\partial }{\partial x^\mu} \left(\frac{\partial {\cal {L}}}{\partial (\partial_\mu\phi_i)} \right)\right]\,\delta \phi_i\, d^4 x = 0,](http://s0.wp.com/latex.php?latex=%5Cdelta+S%3D%5Cint+%5Cleft%5B+%5Cfrac%7B%5Cpartial+%7B%5Ccal+%7BL%7D%7D%7D%7B%5Cpartial+%5Cphi_i%7D+-+%5Cfrac%7B%5Cpartial+%7D%7B%5Cpartial+x%5E%5Cmu%7D+%5Cleft%28%5Cfrac%7B%5Cpartial+%7B%5Ccal+%7BL%7D%7D%7D%7B%5Cpartial+%28%5Cpartial_%5Cmu%5Cphi_i%29%7D+%5Cright%29%5Cright%5D%5C%2C%5Cdelta+%5Cphi_i%5C%2C+d%5E4+x+%3D+0%2C&bg=ffffff&fg=000000&s=0)
que conduce a las ecuaciones de Euler-Lagrange

para cada campo .
.
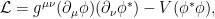
donde
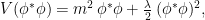
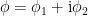 , y
, y  se pueden considerar como dos campos independientes. El parámetro
se pueden considerar como dos campos independientes. El parámetro 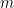 , en la versión cuántica de este campo se convertirá en la masa de las partículas. El parámetro
, en la versión cuántica de este campo se convertirá en la masa de las partículas. El parámetro 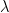 representa la constante de auto-interacción de las partículas del campo consigo mismas.
representa la constante de auto-interacción de las partículas del campo consigo mismas.
Las ecuaciones de Euler-Lagrange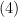 dan
dan


y como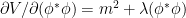 , obtenemos
, obtenemos

para las ecuaciones de este campo relativista. En la versión cuántica de esta teoría estas ecuaciones representan una partícula (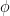 ) y su antipartícula (
) y su antipartícula ( ) de espín 0 (bosón escalar) de masa
) de espín 0 (bosón escalar) de masa 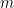 .
.
Tanto la lagrangiana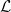 como las ecuaciones de campo son invariantes ante transformaciones de aforo globales,
como las ecuaciones de campo son invariantes ante transformaciones de aforo globales,

es decir, transformaciones de fase o de tipo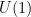 . La invarianza
. La invarianza 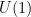 conduce a la conservación de la carga eléctrica. Calculando la 4-divergencia de la densidad de corriente
conduce a la conservación de la carga eléctrica. Calculando la 4-divergencia de la densidad de corriente

obtenemos aplicando las ecuaciones del campo
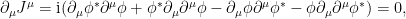
con lo que la carga eléctrica
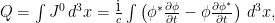
se conserva . Es necesario recurrir a la versión cuántica de la teoría para que en la definición de
. Es necesario recurrir a la versión cuántica de la teoría para que en la definición de 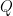 aparezcan
aparezcan  , la carga del electrón, y
, la carga del electrón, y 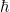 , la constante de Planck, así como para obtener que la carga eléctrica está cuantizada
, la constante de Planck, así como para obtener que la carga eléctrica está cuantizada 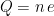 . Nótese que un campo escalar real (
. Nótese que un campo escalar real ( ) representa partículas neutras
) representa partículas neutras  .
.
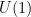 global del campo escalar complejo indica que podemos seleccionar la
fase del campo arbitrariamente, pero si cambiamos la fase en un punto
del espacio debemos hacerlo simultáneamente en todos los puntos. Sin
embargo, esto es incompatible con la relatividad especial, ya que
implica que una señal (el cambio de fase en un punto) ha de propagarse a
una velocidad infinita. Para restaurar la causalidad física debemos
considerar cambios de fase locales, es decir, la teoría con invarianza
de aforo
global del campo escalar complejo indica que podemos seleccionar la
fase del campo arbitrariamente, pero si cambiamos la fase en un punto
del espacio debemos hacerlo simultáneamente en todos los puntos. Sin
embargo, esto es incompatible con la relatividad especial, ya que
implica que una señal (el cambio de fase en un punto) ha de propagarse a
una velocidad infinita. Para restaurar la causalidad física debemos
considerar cambios de fase locales, es decir, la teoría con invarianza
de aforo 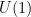 local,
local,

Considerando un cambio infinitesimal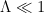 , se obtiene
, se obtiene


con lo que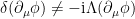 y
y  no se transforma covariantemente, es decir, como lo hace
no se transforma covariantemente, es decir, como lo hace 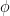 . Por ello, la lagrangiana tampoco es invariante
. Por ello, la lagrangiana tampoco es invariante
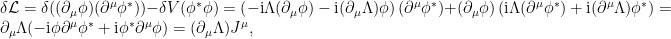
ya que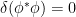 .
.
Para restaurar la invarianza de aforo hay que introducir un campo vectorial (con las mismas unidades que
(con las mismas unidades que  ) acoplado a la corriente
) acoplado a la corriente 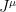 , y que se transforme adecuadamente. Debemos añadir
, y que se transforme adecuadamente. Debemos añadir

con lo que obtenemos el término requerido

pero a costa de introducir un nuevo término a cancelar
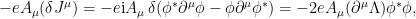
lo que nos obliga a introducir otro término
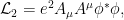
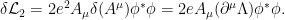
De esta forma es invariante ante transformaciones
es invariante ante transformaciones 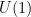 locales.
locales.
El campo vectorial también puede interactuar consigo mismo de forma invariante. Definiendo
también puede interactuar consigo mismo de forma invariante. Definiendo
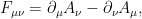

podemos añadir a la lagrangiana

y obtener como lagrangiana total
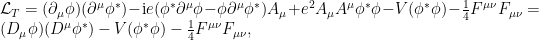
donde hemos introducido la derivada covariante

que se transforma como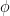 ,
,
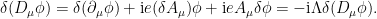
En la lagrangiana total , ha sido necesario introducir de forma natural un campo electromagnético con objeto de garantizar la invarianza
, ha sido necesario introducir de forma natural un campo electromagnético con objeto de garantizar la invarianza 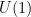 local de la lagrangiana original.
local de la lagrangiana original.
Las ecuaciones de Maxwell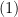 se satisfacen automáticamente para
se satisfacen automáticamente para 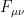 . Las ecuaciones de Euler-Lagrange para el campo
. Las ecuaciones de Euler-Lagrange para el campo 

conducen a las ecuaciones

utilizando como corriente la versión covariante
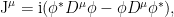
que también se conserva .
.
Es importante notar que el campo electromagnético no tiene masa ( ), ya que el término de masa
), ya que el término de masa
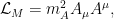
no es invariante ante transformaciones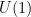 . Por ello, las partículas del campo electromagnético, los fotones, han de viajar a la velocidad de la luz.
. Por ello, las partículas del campo electromagnético, los fotones, han de viajar a la velocidad de la luz.
Finalmente, debemos notar que , la constante de acoplamiento entre el campo electromagnético
, la constante de acoplamiento entre el campo electromagnético  y el campo escalar
y el campo escalar 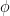 , juega un papel doble. Por un lado, es la carga eléctrica, una cantidad que se conserva
, juega un papel doble. Por un lado, es la carga eléctrica, una cantidad que se conserva 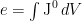 , y por otro lado, mide la fuerza con la que la partícula
, y por otro lado, mide la fuerza con la que la partícula 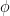 interactúa con el campo electromagnético
interactúa con el campo electromagnético  .
.
 a la que se produce la rotura espontánea de la simetría. El estado físico, o de mínima energía, para
a la que se produce la rotura espontánea de la simetría. El estado físico, o de mínima energía, para 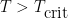 es simétrico, pero para
es simétrico, pero para 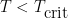 es asimétrico y está infinitamente degenerado ya que la dirección en la
que se alinean los espines se elige prácticamente al azar, si se repite
el experimento de calentar y enfriar muchas veces en todas las
ocasiones se obtienen direcciones norte-sur completamente distintas.
es asimétrico y está infinitamente degenerado ya que la dirección en la
que se alinean los espines se elige prácticamente al azar, si se repite
el experimento de calentar y enfriar muchas veces en todas las
ocasiones se obtienen direcciones norte-sur completamente distintas.
 complejo presentado más arriba. El estado de mínima energía para este campo se determina minimizando el potencial
complejo presentado más arriba. El estado de mínima energía para este campo se determina minimizando el potencial 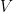 , en concreto,
, en concreto,
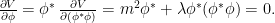
Cuando ,
, 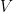 tiene un mínimo para
tiene un mínimo para 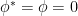 . Pero para
. Pero para  tiene un máximo local en
tiene un máximo local en 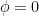 e infinitos mínimos para
e infinitos mínimos para
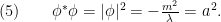
Todos los mínimos se encuentra en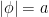 , un círculo en el plano
, un círculo en el plano  , donde
, donde 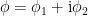 como se muestra en la figura que aparece más arriba.
como se muestra en la figura que aparece más arriba.
En una teoría cuántica,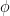 es un operador y la condición de mínima energía determina el valor
esperado del campo en el vacío, es decir, cuando no hay ninguna
partícula
es un operador y la condición de mínima energía determina el valor
esperado del campo en el vacío, es decir, cuando no hay ninguna
partícula

Los estados con una, dos o partículas se obtienen añadiendo estas partículas una a una al vacío, que puede no coincidir con
partículas se obtienen añadiendo estas partículas una a una al vacío, que puede no coincidir con 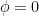 . Tomando coordenadas polares,
. Tomando coordenadas polares,
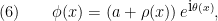
obtenemos para el estado del vacío
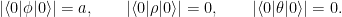
Este campo tiene las mismas características que el ejemplo del ferromagnetismo: tenemos infinitos estados de vacío degenerados que están conectados por la simetría de la teoría, cambiar la fase, de tal forma que la elección de un vacío concreto (como la dirección de magnetización) rompe la simetría, fija una fase dada.
Podemos considerar a y
y 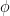 como los campos físicos, con los que expresaremos el lagrangiano
como los campos físicos, con los que expresaremos el lagrangiano  . Operando
. Operando
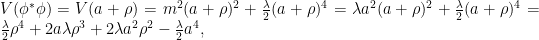
donde se ha usado la ec. , y para el otro término
, y para el otro término
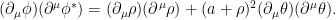
El lagrangiano tiene un término en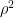 , por lo que el campo $\rho$ tiene una masa dada por
, por lo que el campo $\rho$ tiene una masa dada por , mientras que la ausencia de término en
, mientras que la ausencia de término en  indica que
indica que  es un campo sin masa. Como resultado de una ruptura espontánea de la simetría dos campos escalares con masa (
es un campo sin masa. Como resultado de una ruptura espontánea de la simetría dos campos escalares con masa (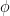 y
y  ) se han convertido en un campo con masa y otro sin ella.
) se han convertido en un campo con masa y otro sin ella.
La Figura de más arriba muestra que, para pequeño, mover el vacío desde el origen hasta el punto
pequeño, mover el vacío desde el origen hasta el punto 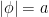 cuesta energía, que se convierte en la masa del campo
cuesta energía, que se convierte en la masa del campo  para
para  . Mover
. Mover  alrededor del círculo de degeneración del vació no cuesta energía, por lo que este campo permanece sin masa. La partícula
alrededor del círculo de degeneración del vació no cuesta energía, por lo que este campo permanece sin masa. La partícula  se denomina bosón de Goldstone. El teorema de Goldstone dice que toda
ruptura de simetría de un teoría cuántica de campos global genera una
partícula de espín cero sin masa.
se denomina bosón de Goldstone. El teorema de Goldstone dice que toda
ruptura de simetría de un teoría cuántica de campos global genera una
partícula de espín cero sin masa.
 complejo acoplado a un campo electromagnético, presentado más arriba. Tomando, con
complejo acoplado a un campo electromagnético, presentado más arriba. Tomando, con  , el campo en forma exponencial
, el campo en forma exponencial 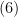 alrededor del estado de mínima energía
alrededor del estado de mínima energía  , obtenemos fácilmente como nueva lagrangiana
, obtenemos fácilmente como nueva lagrangiana

donde hemos eliminado términos de orden superior; la nueva densidad lagrangiana muestra que el campo vectorial , que representaba al fotón, ha adquirido masa (
, que representaba al fotón, ha adquirido masa (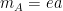 ) “comiéndose” al bosón escalar
) “comiéndose” al bosón escalar  , el bosón de Goldstone, que no tiene existencia física gracias a la simetría
, el bosón de Goldstone, que no tiene existencia física gracias a la simetría 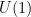 local, mientras que el bosón escalar
local, mientras que el bosón escalar  ,
bosón de Higgs, sigue siendo masivo. A partir de dos bosones escalares
con masa y un bosón vectorial sin masa hemos obtenido, gracias a
la rotura espontánea de la simetría, un bosón vectorial y un bosón
escalar ambos con masa.
,
bosón de Higgs, sigue siendo masivo. A partir de dos bosones escalares
con masa y un bosón vectorial sin masa hemos obtenido, gracias a
la rotura espontánea de la simetría, un bosón vectorial y un bosón
escalar ambos con masa.
En la parte II de este artículo abordaremos el mecanismo de Higgs en teorías de aforo no abelianas con grupos de simetría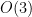 y
y  , lo que nos anticipará su aplicacióin a la teoría electrodébil.
, lo que nos anticipará su aplicacióin a la teoría electrodébil.
A.A. Sokolov et al., “Electrodinámica Cuántica,” Editorial Mir, Moscú (1989).
N. Nélipa, “Physique des Particules Élémentaires,” Editorial Mir, Moscú (1981).
Igor Campillo, físico y Director de Euskampus en la Universidad del País Vasco, Campus de Excelencia Internacional, lo ha dejado más claro que el agua en “La partícula que tu abuela nunca entenderá por mucho que se lo expliques,” Amazings.es, 17 julio 2012. “Me temo que todo este esfuerzo resulta vano desde el punto de vista conceptual, al menos si se aspira a explicar el bosón de Higgs “hasta a mi abuela”… “Comprender es acostumbrarse.” Según aprendemos, lo que nos había parecido inescrutable al principio resulta ser trivial, simplemente por el hecho de trabajar en ello. Por eso resulta tan difícil captar lo que es la mecánica cuántica, porque está fuera de nuestra experiencia cotidiana y uno no se puede acostumbrar a ella utilizando ejemplos de nuestro día a día. Sólo tras mucho operar y calcular, se empiezan a captar sutilezas, conceptos e implicaciones que de otra forma son inimaginables. Entender y explicar el bosón de Higgs sólo puede hacerse dentro del formalismo donde aparece. No podemos hacer “un como si”. No admite traducción e interpretación simultánea.”
¿Qué es el bosón de Higgs? La partícula con la que se puede observar el campo de Higgs. ¿Qué es el campo de Higgs? Un campo con el que interaccionan las partículas que tienen masa. Esta interacción es cuántica, pero podemos hacernos una idea de cómo funciona utilizando la teoría clásica de campos. Nos lo cuenta The Unapologetic Mathematician en “The Higgs Mechanism part 1: Lagrangians,” July 16, “The Higgs Mechanism part 2: Examples of Lagrangian Field Equations,” July 17, “The Higgs Mechanism part 3: Gauge Symmetries,” July 18, y “The Higgs Mechanism part 4: Symmetry Breaking,” July 19. Recomiendo una lectura a estas entradas.
He pensado en traducir dichas entradas, pero no tengo tiempo y ya hice algo parecido hace algún tiempo (abril de 1999). Quizás conviene recordarlo.

Figura 1: Potencial V(|φ|²) para m²>0 (gráfica izquierda) y m²<0 (gráfica derecha).
Generación de la Masa de las Partículas. I: Bosones Escalares de Goldstone y Higgs
El premio Nobel de Física de 1999 fue concedido a los físicos holandeses Gerard ‘t Hooft y Martinus Veltman por sus contribuciones a la renormalización de la teoría electrodébil y, con ella, de todo el Modelo Estándar de las partículas elementales. En el Modelo Estándar las masas de las partículas elementales se generan mediante una rotura espontánea de la simetría.La rotura espontánea de la simetría fue descubierta por Heisenberg en 1932 en su estudio de los materiales ferromagnéticos, y aplicada por Nambu y Goldstone, a principios de los 1960, a teorías de campos en física de la materia condensada (teorías de aforo (gauge) global). En 1964, Higgs (y otros autores) la aplicó a teorías de aforo local descubriendo un mecanismo para la generación de la masa de las partículas elementales. Dicho mecanismo está en la base de la teoría electrodébil, desarrollada por Glashow, Weinberg y Salam, premios Nobel de Física en 1979. La teoría electrodébil es una teoría de aforo local
‘t Hooft probó en su tesis doctoral, dirigida por Veltman, que una teoría de aforo local con rotura espontánea de la simetría, como la teoría electrodébil, es renormalizable. De esta forma se definió un procedimiento consistente para realizar cálculos de gran precisión en esta teoría y, entre ellos, la predicción de las masas de las partículas
En este artículo se estudiará la generación de masa mediante rotura espontánea de la simetría utilizando una teoría clásica de campos. Primero, repasaremos brevemente la notación tensorial (de índices) para vectores y covectores, la relatividad especial, la diferencia entre vectores axiales y polares, y la formulación covariante o relativista de las ecuaciones de Maxwell. Seguidamente, repasaremos la formulación lagrangiana de campos clásicos y su aplicación a un campo escalar cargado (complejo) que tiene simetría de aforo global de tipo
Vectores y covectores
Sea un vectordonde en la última expresión hemos usado el convenio de suma de índices repetidos de Einstein, según el cual los términos (productos) con índices repetidos representan la suma de dichos términos respecto a dichos índices.
Se denomina espacio vectorial dual
donde
Asociada a la base de vectores
donde
donde hemos usado que los índices son mudos. La dimensión de
El espacio-tiempo euclídeo
Galileo, que son las que dejan invariante el tiempo y la distancia euclídea en el espacio, definida mediante el producto escalar euclídeo
Como
Para distancias infinitesimales obtenemos la condición
Relatividad especial
La relatividad especial se basa en el principio de constancia de la velocidad de la luz (Al contrario que en el espacio-tiempo euclídeo, los vectores contravariantes y los covariantes en el espacio de Minkowski tienen componentes que difieren (aunque solo en su signo), en concreto,
respectivamente. Introduciendo el tensor métrico fundamental
podemos escribir la métrica como
Se definen los operadores diferenciales
que conducen al operador de segundo orden
de d’Alembert, que es invariante Lorentz.
Vectores polares y axiales
Un vector (o un campo vectorial)Introduciendo el tensor completamente antisimétrico de rango 3 de Levi-Civita
se escribe el producto vectorial
Asociado al producto vectorial podemos escribir un tensor anti-simétrico de rango 2 de la forma
Así, para el rotacional
En general, todos los vectores axiales
Formulación covariante de las ecuaciones de Maxwell
Las ecuaciones de Maxwell para el campo electromagnético (con unidades en el sistema gaussiano) toman la formadonde
Las ecuaciones
(ya que
En relatividad especial podemos definir un cuadrivector potencial
Definiendo el tensor covariante antisimétrico
obtenemos que, de lo dicho anteriormente,
Definiendo un cuadritensor completamente antisimétrico de cuarto rango
donde
Introduciendo un cuadrivector corriente
Además, se cumple automáticamente la ecuación de continuidad
A partir del tensor del campo
que indican que la energía se conserva y el campo electromagnético es transversal, respectivamente.
El campo electromagnético es invariante ante transformaciones de aforo (gauge) de tipo
Teoría clásica de campos
En teoría de campos relativistas se especifican las ecuaciones para los camposdonde
e integrando por partes usando
que conduce a las ecuaciones de Euler-Lagrange
para cada campo
Campo escalar complejo con potencial no lineal cuártico
Consideremos un campo escalar complejo con una auto-interacción no lineal cuártica,donde
Las ecuaciones de Euler-Lagrange
y como
para las ecuaciones de este campo relativista. En la versión cuántica de esta teoría estas ecuaciones representan una partícula (
Tanto la lagrangiana
es decir, transformaciones de fase o de tipo
obtenemos aplicando las ecuaciones del campo
con lo que la carga eléctrica
se conserva
Teoría de aforo local para el campo escalar complejo
La invarianzaConsiderando un cambio infinitesimal
con lo que
ya que
Para restaurar la invarianza de aforo hay que introducir un campo vectorial
con lo que obtenemos el término requerido
pero a costa de introducir un nuevo término a cancelar
lo que nos obliga a introducir otro término
De esta forma
El campo vectorial
podemos añadir a la lagrangiana
y obtener como lagrangiana total
donde hemos introducido la derivada covariante
que se transforma como
En la lagrangiana total
Las ecuaciones de Maxwell
conducen a las ecuaciones
utilizando como corriente la versión covariante
que también se conserva
Es importante notar que el campo electromagnético no tiene masa (
no es invariante ante transformaciones
Finalmente, debemos notar que
Rotura espontánea de la simetría
La rotura espontánea de la simetría la descubrió Heisenberg trabajando con materiales ferromagnéticos, imanes naturales. A baja temperatura, todos los espines, pequeños dipolos magnéticos asociados a los átomos del material, están alineados en una determinada dirección, la de norte-sur del imán, y el material no es simétrico cuando lo rotamos (de ahí que las brújulas siempre apunten al norte aunque las giremos). A alta temperatura, la magnetización desaparece, los espines se alinean en direcciones aleatorias y el material se vuelve simétrico, no cambia cuando lo rotamos. Existe una temperatura críticaBosón de Goldstone
Estudiaremos ahora, la aplicación de la ruptura espontánea de la simetría al campo escalarCuando
Todos los mínimos se encuentra en
En una teoría cuántica,
Los estados con una, dos o
obtenemos para el estado del vacío
Este campo tiene las mismas características que el ejemplo del ferromagnetismo: tenemos infinitos estados de vacío degenerados que están conectados por la simetría de la teoría, cambiar la fase, de tal forma que la elección de un vacío concreto (como la dirección de magnetización) rompe la simetría, fija una fase dada.
Podemos considerar a
donde se ha usado la ec.
El lagrangiano tiene un término en
La Figura de más arriba muestra que, para
Bosón de Higgs
El mecanismo de Higgs consiste en aplicar una rotura de simetría a un campo con simetría de aforo local. Consideremos el campo escalardonde hemos eliminado términos de orden superior; la nueva densidad lagrangiana muestra que el campo vectorial
En la parte II de este artículo abordaremos el mecanismo de Higgs en teorías de aforo no abelianas con grupos de simetría
Bibliografía
L.H. Ryder, “Quantum Field Theory,” (2nd. ed.), Cambridge University Press (1996).A.A. Sokolov et al., “Electrodinámica Cuántica,” Editorial Mir, Moscú (1989).
N. Nélipa, “Physique des Particules Élémentaires,” Editorial Mir, Moscú (1981).
Suscribirse a:
Comentarios (Atom)

