Otro trabajo apunta que la función de ondas describe
plenamente la realidad física y deja de lado las interpretaciones
subjetivas de la misma.
En Física muchas veces no estamos muy seguros sobre si algo algo
tiene existencia propia por sí mismo o es un modelo de la realidad.
Digamos que en el primer caso se trataría de un hecho ontológico y en el
segundo caso de algo más bien epistemológico.
Creemos que los átomos son reales, así que tendrían existencia
ontológica, de hecho, incluso ya los podemos ver con distintas técnicas.
Sin embargo, hay modelos que han ido explicando el comportamiento de
los átomos y que se han sucedido unos a otros. Según el más moderno
explicaba mejor que el anterior los datos experimentales lo sustituía.
Ya nadie utiliza el modelo de Borh para explicar el átomo de uranio y
mucho menos el modelo de Thomson.
La gravedad (como la evolución) es un hecho. Si usted tiene dudas sobre
ese hecho ontológico pruebe a subir a un edificio muy alto y lanzarse al
vacío. Le garantizo que al final ya no tendrá ninguna duda al respecto
(ni sobre la gravedad ni sobre cualquier otra cosa). Sin embargo, para
explicar la gravedad tenemos varios modelos.
Podemos conformarnos con la gravedad newtoniana o usar la Relatividad
General (que sigue siendo clásica y no cuántica). Ambas explican la
gravedad bastante bien en sus respectivos regímenes. Pero si queremos
explicar el desplazamiento anómalo del perihelio de Mercurio no tenemos
más remedio que usar la Relatividad General (RG). Por desgracia, no
contamos todavía con una teoría cuántica de gravedad, así que no podemos
afirmar muchas más cosas. Se ha propuesto que la gravedad estaría
mediada por una partícula de
spin 2 denominada gravitón. Si
esto es así, ¿en que lugar quedaría la distorsión del espacio-tiempo que
propone la RG? ¿Es esa distorsión un mero modelo de realidad para
realizar cálculos y en realidad tal distorsión no existe? ¿Es la
distorsión espacio-temporal real y ontológica mientras que los
gravitones son epistemológicos? ¿Existen realmente los gravitones o como
máximo son sólo cuasipartículas conceptuales? Podremos creer en lo que
dice la RG o creer en los gravitones, pero no en los dos a la vez, al
menos desde el punto de vista ontológico. Epistemológicamente podemos
creer en ambos a la vez.
Incluso cuando nos vamos a la Física de Altas Energías surgen las dudas
sobre la ontología de la existencia de ciertas partículas. En los
propios sistemas de detección e informáticos se presuponen cosas y se
admiten ciertos modelos de tal modo que al final quizás tal o cual
partícula realmente no exista y sólo tengamos un modelo de algo, aunque
la hayamos “detectado”. Obviamente este punto no es compartido por los
físicos que trabajan en el LHC y similares, pues su modo de pensar (y de
vida) está ya asimilado por el sistema.
Demostrar cualquiera de lo puntos anteriores es muy difícil, pues el
método científico permite comprobar modelos de realidad y no distingue
entre comprobar modelos y comprobar entes “reales”. No suele haber datos
experimentales o experimentos que distingan una situación de otra.
Este problema es aún más acusado cuando abandonamos el mundo clásico y
nos adentramos en el cuántico. Aquí el problema no está en los objetos
que se describen, sean átomos, electrones o
quarks, sino en el
marco teórico mismo. La Mecánica Cuántica (MC) funciona tan bien para
calcular cantidades que durante 80 años casi se han dejado de lado sus
aspectos fundacionales. El problema de interpretación de la MC se
acarrea desde los inicios de la misma.
En MC se asignan funciones de onda Ψ al estado de los objetos cuánticos y
se calculan valores esperados de un observable a través de un operador
autoadjunto. La posición
x de una partícula es un observable y le corresponde un operador autoadjunto, la cantidad de movimiento
p
también. El tiempo, sin embargo, no es un observable, sino que aparece
en la ecuación de evolución (la ecuación de Schrödinger). Esta ecuación
nos dice que si en un instante Ψ corresponde a un estado determinado al
cabo de un tiempo corresponderá a otro según dicha ecuación.
Además, las funciones de ondas matemáticamente “viven” en un espacio
abstracto de dimensión infinita denominado “espacio de Hilbert”.
Si queremos calcular la posición de una partícula en un sistema cuántico
en un momento dado tendremos que calcular el valor esperado del
operador x mediante una operación que podríamos definir como
“estadística”. En su versión más sencilla tal cosa se simboliza así:
< ψ|x|ψ>. Digamos que la función de onda se usa para calcular los
valores de cosas que sí se pueden medir, pero la función de ondas en sí
no se puede medir, aunque sí calcular.
Si seguimos con nuestro ejemplo de la posición, nos tenemos que dar
cuenta de que al ser un cálculo probabilístico no obtenemos la posición
exacta de la partícula, sino su posición más probable. La función de
onda de la partícula es extensa, no puntual, y tiene un valor dado (que
puede ser incluso en el plano complejo) para cada punto del espacio y
evoluciona en el tiempo según la ecuación de Schrödinger. Bajo este
punto de vista en realidad no hay una “partícula puntual” sino algo
extenso sobre lo que se pueden calcular cosas, como la posición más
probable de una “partícula” si imponemos que tiene que ser como un
punto, aunque no sea tal punto. Se puede decir que la función de ondas
es algo “borroso” que al medir colapsa a un valor determinado.
Recordemos aquí que el colapso de la función de ondas no es lo mismo que
el valor esperado de un observable, ni en el mundo físico ni
matemáticamente (una proyección sobre un subespacio de Hilbert o un
valor esperado respectivamente)
Usando la función de ondas podemos calcular el comportamiento de los
sistemas cuánticos, pero sólo con cierta probabilidad. Esta naturaleza
probabilística difiere de cómo los físicos describen el mundo clásico no
microscópico.
Es ahora cuando tenemos el problema de interpretación de la MC, algo que
se remonta a los años treinta del pasado siglo (e incluso antes).
Podemos asumir que la función de ondas es un objeto que representa una
realidad física (visión ontológica) o asumir que sólo representa el
conocimiento subjetivo que el observador tiene sobre la realidad (visión
epistemológica).
En el primer caso la función de ondas corresponde a un elemento de la
realidad que existe objetivamente, tanto si el observador mide como si
no lo hace. Mientras que en la otra visión la función de ondas no
representa la realidad, sino el conocimiento subjetivo del observador
acerca de una realidad que está por debajo. La interpretación de
Copenhague es precisamente esta última y la función de onda no es más
que cierta idea de probabilidad que sólo asume un valor real cuando el
observador realiza una medición del sistema.
A partir de este y otros problemas fue cuando Einstein, Podolsky y Rosen
afirmaron que la función de ondas no proporcionaba una descripción
completa de la realidad física y que la MC era incompleta. Debía de
haber una información inaccesible (variables ocultas) que nos obligaba a
calcular probabilidades, tal y como se hace en Física Estadística, y la
realidad última sería clásica. Si así fuera Dios no jugaría a los
dados.
Hace unos meses llegó a Nature un estudio que apunta a la primera
posibilidad. Sus autores mostraban que una interpretación subjetiva de
la función de ondas violaría ciertas asunciones plausibles
[1].
Ahora un trabajo publicado en Physical Review Letters de Roger Colbeck
y Renato Renner (Perimeter Institute y ETH Zurich respectivamente)
apunta en la misma dirección: la función de ondas representa la realidad
objetiva. Es decir, es un elemento de realidad del sistema.
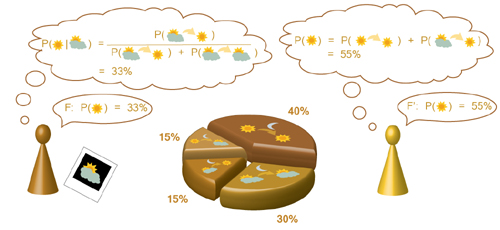
Para apoyar su punto de vista usan una analogía sobre la predicción del
tiempo atmosférico que reproducimos a continuación casi como viene en el
artículo. Según esta analogía habría dos meteorólogos tratando de
predecir el tiempo que hará mañana en un lugar. Por ejemplo, que será
nuboso con una probabilidad del 67% y soleado con una probabilidad del
33% (ver ilustración de cabecera). La Mecánica Clásica describe con
precisión los procesos relevantes que se dan en este sistema, así que el
tiempo que hará mañana se podrá calcular determinísticamente a partir
de las condiciones iniciales que se den ahora. El hecho de que la
predicción sea en realidad probabilística refleja la carencia de
conocimiento de los meteorólogos sobre parte de las condiciones
iniciales. La predicción meteorológica no es pues un elemento de la
realidad asociada con la atmósfera, sino que refleja el conocimiento
subjetivo del que hace la predicción. Un segundo meteorólogo con un
conocimiento diferente sobre las condiciones iniciales puede llegar a un
pronóstico distinto.
Si ahora nos fijamos en la MC nos podemos preguntar si la función de
ondas Ψ, que asignamos al estado de un sistema cuántico, tiene que ser
vista como un objeto subjetivo como el pronóstico meteorológico o si es
un elemento de la realidad del sistema (una Ψ ontológica).
El problema es que la MC es inherentemente probabilística, incluso
teniendo una descripción completa de la función de ondas del sistema. La
teoría no nos permite predecir el resultado de un medida con certeza.
Esto ha motivado interpretaciones subjetivas de la MC como la de
Copenhague. Según esta visión Ψ sería un mero objeto matemático usado
para calcular cosas. Sería una Ψ epistemológica.
Estos autores ya mostraron recientemente
[2]
que, bajo ciertas asunciones de libre elección y si la MC es correcta,
entonces la MC es “no extensible” en el sentido de que ser máximamente
informativa acerca de lo que se puede obtener en las medidas. Toda
información en la lista de elementos de realidad esta ya contenida en la
función de ondas. Esto es, la función de ondas incluye todos los
elementos de la realidad.
En este nuevo trabajo
[3]
muestran que la lista de elementos de la realidad incluye la función de
ondas. Por tanto, la función de ondas de un sistema cuántico se puede
poner en correspondencia uno a uno o con los elementos de la realidad,
esto es, con las variables que describen el comportamiento del sistema.
Para ello sólo se necesita asumir que los parámetros de medición pueden
ser elegidos libremente y que la teoría produce una predicción
estadística correcta. Estos dos aspectos están siempre implícitos en la
Física.
|
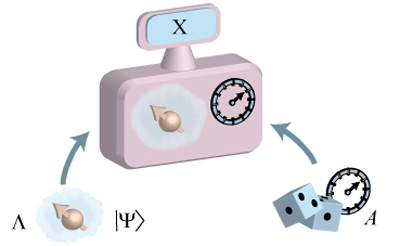
El razonamiento es más o menos como sigue (ver dibujo de arriba). Si
un sistema es preparado en un estado cuántico particular Ψ, el conjunto o
lista de los elementos de la realidad, denotado por Λ, dependen de esa
preparación. Una determinada disposición de medidas A es elegida al azar
y se produce un resultado X. Se puede asumir que Λ es completa para la
descripción del sistema en el sentido de que no hay otros parámetros
que produzcan información adicional acerca del resultado de cualquier
medida elegida. En particular, Ψ no proporciona más información que Λ
acerca de un resultado. La no-extensibilidad de la MC implica, además,
que Λ no puede proporcionar más información acerca de un resultado que
Ψ. Tomados estos dos argumentos juntos se concluye que Λ y Ψ son
informativamente equivalentes. Además, si se tiene en cuenta el hecho de
que estados cuánticos diferentes generalmente dan medidas estadísticas
diferentes, entonces se puede concluir que Ψ debe ser incluida en el
conjunto o lista Λ y por tanto ser considerada un elemento de realidad
del sistema.
La función de ondas incluye, por tanto, toda la información acerca del
sistema que en principio está disponible y que no hay nada que se escapa
(a diferencia del meteorólogo que no dispone de toda la información).
Pese a todo, una medida nos proporcionará una valor con cierta
aleatoridad, lo que significa que la Naturaleza es inherentemente
probabilística a ese nivel.
En la analogía de los meteorólogos los datos y el modelo usados por
ellos serían la función de onda y la realidad se correspondería con el
tiempo presente (nublado, lluvioso, soleado, etc.). Si en esa analogía
hubiera una correspondencia uno a uno (como la que proponen estos
físicos para el caso de la MC) entre los datos meteorológicos y el
tiempo meteorológico, entonces estaríamos en una buena situación, pues
el pronóstico (aunque esta predicción sea probabilística) serían tan
preciso como máximamente puede ser, en el sentido de que no hay
información extra que nos falte. No sabremos exactamente el tiempo que
hará mañana, pero nuestro pronóstico será el mejor posible. Recordemos
una vez más que la MC es determinista en su evolución porque la ecuación
de Schrödinger lo es, así que la analogías no es perfecta. La
aleatoriedad de la MC no está en su evolución del presente al futuro,
sino en la medida, sea ahora o mañana. Es aleatoria incluso en el
momento actual en el que se tiene toda la información y el paso del
tiempo no mejora ni empeora sustancialmente tal problema.
Los autores afirman que su resultado es definitivo si se acepta el
principio de libre elección. Sin embargo, sería legítimo cuestionar esta
asunción y por eso ya trabajan en una demostración en la que la libre
elección puede ser reemplazada por una premisa más débil, una libertad
de elección parcial. Estos prerrequisitos más débiles serían una
causalidad local y que sólo se requiera que la elección sea
independiente de parámetros ocultos preexistentes (en el sentido que ya
hizo Bell en su tiempo).
Los asuntos de interpretación de la MC son arenas movedizas que en
general no suelen ser falsables. Sin embargo, Colbeck y Renner
argumentan que los resultados experimentales podrían avalar sus
resultados. Aunque en el caso de la libre elección admiten que la cosa
sería más complicada, sostienen que aún así se podría falsar en algunos
casos.
Copyleft: atribuir con enlace a
http://neofronteras.com/?p=3822
Fuente de los dibujos: Colbeck y Renner