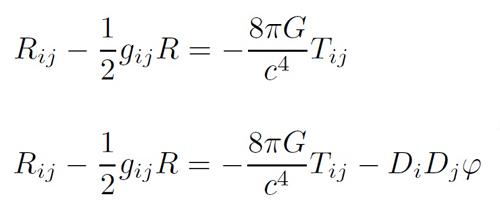Fuente: Neofronteras
Según un estudio las ecuaciones de Einstein pueden tener un
grado de impredecibilidad aún mayor que el de los sistemas caóticos.
Incluso conociendo con precisión infinita las condiciones iniciales no
se puede predecir el futuro estado del sistema para determinados
modelos.
Las ecuaciones de campo de Einstein de la Relatividad General
describen el comportamiento del espacio en presencia de masa y/o energía
y proporciona la mejor teoría que tenemos para describir la gravedad.
El problema es que la gravedad gravita y esto se ve reflejado en las ecuaciones como una “retroalimentación” en las mismas. En otras palabras, estas ecuaciones son muy difíciles de resolver analíticamente con lápiz y papel o incluso numéricamente. En general las ecuaciones diferenciales en derivadas parciales son muy difíciles de resolver, incluso cuando sean sencillas (las de Einstein no lo son).
La consecuencia de ello es que conocemos sólo unos pocos casos de soluciones generales para este tipo de ecuaciones (ecuación del calor, ecuación de la cuerda vibrante, ecuación de Schrödinger…). Las demás, simplemente, no sabemos resolverlas. Sin embargo, cuando las condiciones de contorno y las condiciones iniciales son especiales puede que tengamos ciertas simetrías que permitan resolver la ecuación.
En el caso de las ecuaciones de Einstein se conocen unas cuantas soluciones, como la de Schwarzschild para agujeros negros o para modelos de tipo Friedmann-Robertson-Walker en Cosmología. Las ecuaciones de Einstein hacen honor con su nombre al famoso sabio, pero incluso sus soluciones hacen honor al físico que las descubre (aunque su apellido casi no tenga vocales).
Por otro lado, hay sistemas caóticos deterministas que nos impredecibles. Poseen lo que se llama “efecto mariposa” en alusión a la analogía que dice que el batir de alas de una mariposa en la selva brasileña puede producir una gran tormenta en Indonesia (bueno, hay muchas versiones). Este efecto tiene que ver con la estabilidad de la las ecuaciones. Básicamente si un sistema es caótico, como el tiempo atmosférico, es predeciblemente impredecible. Sólo con una precisión infinita en las condiciones iniciales y un cálculo con esa precisión se podría determinar el estado final de uno de estos sistemas. Pero nunca tenemos esa precisión infinita.
Cuando el caos determinista se puso de moda todo físico aburrido quería encontrar si tal o cual modelo era caótico. También hubo algunos que estudiaron si las ecuaciones de campo de Einstein eran caóticas, como Belinski, Khalatnikov y Lifshitz en los setenta.
El caos encontrado en las ecuaciones de Einstein no era para preocuparse, pues asumía unas condiciones de inhomogeneidad que no se dan en el Universo. Los modelos de Friedmann-Robertson-Walker que se usan en Cosmología asumen un Universo homogéneo e isótropo.
Ahora, un par de físicos italianos hacen un estudio heurístico sobre el asunto y llegan a la conclusión de que las ecuaciones de Einstein pueden tener un grado de impredecibilidad aún mayor que el de los sistemas caóticos. Incluso conociendo con precisión infinita las condiciones iniciales no se puede predecir el futuro estado del sistema. Es más, si están en lo cierto, los modelos cosmológicos podrían ser indecibles en el sentido gödelinao. Según ellos serían comparables a máquinas de Turing en el sentido de que incluso con unas condiciones iniciales conocidas exactamente la evolución de este tipo de sistemas dinámicos sería impredecible.
Recordemos de que Kurt Gödel es el matemático que descubrió uno de los resultados más grandes, inesperados y fascinantes de las Matemáticas: el teorema de incompletitud. Según este teorema todo sistema axiomático formal (una manera elegante y rigurosa de definir a las Matemáticas) contiene enunciados que no pueden ser demostrados ni refutados. Si se incorporan como verdaderos (o falsedades) entonces se tiene otro sistema que a su vez contendrá otros enunciados que también serán indecidibles. Al final se crean distintas Matemáticas dependiendo de la elección realizada.
Gödel murió de hambre debido a una paranoia de envenenamiento una que vez su mujer falleció (única que sabía llevarlo) y ni el propio Einstein, amigo personal de Gödel, pudo hacer nada por evitarlo.
El asunto de la indecibilidad puede afectar la estabilidad de las ecuaciones diferenciales y en trabajos previos se ha estudiado el asunto, pero generalmente no eran ecuaciones que describieran aspectos físicos.
Yves Gaspar y Giovanni Acquaviva realizan un estudio heurístico y reconocen que haría falta un estudio rigurosos del asunto. Quieren simplemente que su trabajo de pie a trabajos posteriores en modelos inhomogéneos de las ecuaciones de Einstein. Así que, de momento, no se tambalean los cimientos de la Física.
Según ellos su trabajo muestra que la indecibilidad puede aparecer en problemas físicos importantes, como es el estudio de las condiciones iniciales en cosmología. Según ellos para modelos de Bianchi de tipo VIII la cuestión de si un conjunto de condiciones iniciales cerca de la singularidad inicial da lugar a comportamiento caótico es indecidible.
Si asumimos esto, incluso conociendo las condiciones iniciales con exactitud no se puede predecir la dinámica futura.
El que no se puedan resolver las ecuaciones de los modelos de Bianchi de tipo VIII implica no solamente errores cuantitativos en el cálculo de la evolución futura del sistema, como es habitual, sino que el error puede corresponder a un intercambio entre comportamiento caótico y no caótico. Además habría una presencia de conjuntos de fractales no recursivos. La estabilidad de este tipo de modelos, por tanto, sería indecidible.
Es decir, ni sabiendo con exactitud las condiciones iniciales del Universo se podría predecir totalmente su dinámica futura.
Según estos físicos se podría argumentar que la presencia de la singularidad inicial es crucial para que aparezca esta indecibilidad y que eliminando esta singularidad desaparecería el problema, pero según ellos no es así. La manera de deshacerse de las singularidades suele basarse en asumir que una teoría cuántica de la gravedad no presentaría este tipo de objetos, pero entonces los fenómenos cuánticos introducirían una impredecibilidad cuántica y el cálculo de la función de ondas se hace incomputable.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=3925
Fuentes y referencias:
Artículo en ArXiv.
|
El problema es que la gravedad gravita y esto se ve reflejado en las ecuaciones como una “retroalimentación” en las mismas. En otras palabras, estas ecuaciones son muy difíciles de resolver analíticamente con lápiz y papel o incluso numéricamente. En general las ecuaciones diferenciales en derivadas parciales son muy difíciles de resolver, incluso cuando sean sencillas (las de Einstein no lo son).
La consecuencia de ello es que conocemos sólo unos pocos casos de soluciones generales para este tipo de ecuaciones (ecuación del calor, ecuación de la cuerda vibrante, ecuación de Schrödinger…). Las demás, simplemente, no sabemos resolverlas. Sin embargo, cuando las condiciones de contorno y las condiciones iniciales son especiales puede que tengamos ciertas simetrías que permitan resolver la ecuación.
En el caso de las ecuaciones de Einstein se conocen unas cuantas soluciones, como la de Schwarzschild para agujeros negros o para modelos de tipo Friedmann-Robertson-Walker en Cosmología. Las ecuaciones de Einstein hacen honor con su nombre al famoso sabio, pero incluso sus soluciones hacen honor al físico que las descubre (aunque su apellido casi no tenga vocales).
Por otro lado, hay sistemas caóticos deterministas que nos impredecibles. Poseen lo que se llama “efecto mariposa” en alusión a la analogía que dice que el batir de alas de una mariposa en la selva brasileña puede producir una gran tormenta en Indonesia (bueno, hay muchas versiones). Este efecto tiene que ver con la estabilidad de la las ecuaciones. Básicamente si un sistema es caótico, como el tiempo atmosférico, es predeciblemente impredecible. Sólo con una precisión infinita en las condiciones iniciales y un cálculo con esa precisión se podría determinar el estado final de uno de estos sistemas. Pero nunca tenemos esa precisión infinita.
Cuando el caos determinista se puso de moda todo físico aburrido quería encontrar si tal o cual modelo era caótico. También hubo algunos que estudiaron si las ecuaciones de campo de Einstein eran caóticas, como Belinski, Khalatnikov y Lifshitz en los setenta.
El caos encontrado en las ecuaciones de Einstein no era para preocuparse, pues asumía unas condiciones de inhomogeneidad que no se dan en el Universo. Los modelos de Friedmann-Robertson-Walker que se usan en Cosmología asumen un Universo homogéneo e isótropo.
Ahora, un par de físicos italianos hacen un estudio heurístico sobre el asunto y llegan a la conclusión de que las ecuaciones de Einstein pueden tener un grado de impredecibilidad aún mayor que el de los sistemas caóticos. Incluso conociendo con precisión infinita las condiciones iniciales no se puede predecir el futuro estado del sistema. Es más, si están en lo cierto, los modelos cosmológicos podrían ser indecibles en el sentido gödelinao. Según ellos serían comparables a máquinas de Turing en el sentido de que incluso con unas condiciones iniciales conocidas exactamente la evolución de este tipo de sistemas dinámicos sería impredecible.
Recordemos de que Kurt Gödel es el matemático que descubrió uno de los resultados más grandes, inesperados y fascinantes de las Matemáticas: el teorema de incompletitud. Según este teorema todo sistema axiomático formal (una manera elegante y rigurosa de definir a las Matemáticas) contiene enunciados que no pueden ser demostrados ni refutados. Si se incorporan como verdaderos (o falsedades) entonces se tiene otro sistema que a su vez contendrá otros enunciados que también serán indecidibles. Al final se crean distintas Matemáticas dependiendo de la elección realizada.
Gödel murió de hambre debido a una paranoia de envenenamiento una que vez su mujer falleció (única que sabía llevarlo) y ni el propio Einstein, amigo personal de Gödel, pudo hacer nada por evitarlo.
El asunto de la indecibilidad puede afectar la estabilidad de las ecuaciones diferenciales y en trabajos previos se ha estudiado el asunto, pero generalmente no eran ecuaciones que describieran aspectos físicos.
Yves Gaspar y Giovanni Acquaviva realizan un estudio heurístico y reconocen que haría falta un estudio rigurosos del asunto. Quieren simplemente que su trabajo de pie a trabajos posteriores en modelos inhomogéneos de las ecuaciones de Einstein. Así que, de momento, no se tambalean los cimientos de la Física.
Según ellos su trabajo muestra que la indecibilidad puede aparecer en problemas físicos importantes, como es el estudio de las condiciones iniciales en cosmología. Según ellos para modelos de Bianchi de tipo VIII la cuestión de si un conjunto de condiciones iniciales cerca de la singularidad inicial da lugar a comportamiento caótico es indecidible.
Si asumimos esto, incluso conociendo las condiciones iniciales con exactitud no se puede predecir la dinámica futura.
El que no se puedan resolver las ecuaciones de los modelos de Bianchi de tipo VIII implica no solamente errores cuantitativos en el cálculo de la evolución futura del sistema, como es habitual, sino que el error puede corresponder a un intercambio entre comportamiento caótico y no caótico. Además habría una presencia de conjuntos de fractales no recursivos. La estabilidad de este tipo de modelos, por tanto, sería indecidible.
Es decir, ni sabiendo con exactitud las condiciones iniciales del Universo se podría predecir totalmente su dinámica futura.
Según estos físicos se podría argumentar que la presencia de la singularidad inicial es crucial para que aparezca esta indecibilidad y que eliminando esta singularidad desaparecería el problema, pero según ellos no es así. La manera de deshacerse de las singularidades suele basarse en asumir que una teoría cuántica de la gravedad no presentaría este tipo de objetos, pero entonces los fenómenos cuánticos introducirían una impredecibilidad cuántica y el cálculo de la función de ondas se hace incomputable.
Copyleft: atribuir con enlace a http://neofronteras.com/?p=3925
Fuentes y referencias:
Artículo en ArXiv.
Salvo que se exprese lo contrario esta obra está bajo una licencia Creative Commons.