Qué es el espín de una partícula

Fuente: Francis (th)E mule

Para explicar la estructura fina de los niveles de energía de los electrones en el átomo de hidrógeno, Uhlenbeck y Goudsmit [1] propusieron como hipótesis que el electrón, además de masa y carga, tenía un momento angular intrínseco (el espín) y por tanto un momento magnético. Pauli [2] introdujo la formulación matemática del espín en el contexto de la mecánica cuántica no relativista, asumiendo que sus valores son semienteros y que la función de onda tiene dos componentes, pero sin ofrecer una explicación de su origen. El origen “natural” del espín es la combinación de la relatividad y la cuántica en la ecuación de Dirac para el electrón [3]. La función de onda en mecánica cuántica es un vector en un espacio de Hilbert y la invariancia relativista ante transformaciones del grupo de Poincaré (el grupo inhomogenéo de Lorentz) requiere que las componentes de la función de onda pertenezcan a una representación irreducible de dicho grupo, como afirma el teorema de Wigner [4], que se basó en trabajos matemáticos previos (como los de Weyl [5]). Para una partícula de espín arbitrario, la ecuación cuántica relativista fue obtenida por Majorana (1932), Dirac (1936) y Proca (1936). Por tanto, una partícula tiene un espín s si la función de onda que representa sus estados tiene 2s+1 componentes (donde por componentes entendemos funciones de tipo espinor en el caso de espín semientero y funciones complejas en el caso de espín entero). Explicar el espín sin utilizar las matemáticas de la teoría de grupos aplicada a la mecánica cuántica es casi imposible, igual que lo es explicar el origen del momento angular en mecánica clásica.

¿Por qué el espín tiene las mismas unidades que el momento angular? Porque su origen es similar; el momento angular tiene su origen en la invariancia ante el grupo de rotaciones en el espacio de un sistema cuántico, por lo que la función de onda que lo representa debe ser una representación irreducible de dicho grupo. Las componentes del momento cumplen las leyes del álgebra de Lie so(3) asociada al grupo de Lie SO(3) de las rotaciones en el espacio. Las componentes del espín también cumplen las leyes de un álgebra de Lie, sl(2,C), asociada al grupo de Lorentz SO(1,3). Como el momento angular está asociado al grupo de rotaciones, su interpretación clásica como un “giro” es natural, sin embargo, dicha interpretación clásica para el espín no tiene sentido (salvo que hablemos de un “giro” en un espacio abstracto o espacio interno). En mi opinión, no ayuda nada a la intuición clásica el imaginar como “giros” las transformaciones de Lorentz entre sistemas de referencia inerciales; sin embargo, quizás ayude a algunos lectores, en dicho caso, hay que imaginar el momento angular y el espín como asociados a los “giros” tetradimensionales en el espacio de Minkowski.
Imaginar un electrón como una partícula “puntual” girando, aunque sea  solo porque las unidades del espín son las mismas que las del momento angular, yo creo que no ayuda a la intuición clásica sobre su origen. En mi opinión, debemos aceptar que el espín es un concepto cuántico relativista sin análogo clásico no relativista. A mí me gusta decir que el espín está asociado al hecho de que la función de onda de una partícula relativista tiene varias componentes, es decir, el campo asociado a dicha partícula corresponde a varios “campos componentes” acoplados, como el campo electromagnético corresponde a campos eléctricos y magnéticos acoplados (o “unificados”). Mucha gente me dice que esta descripción es demasiado abstracta y no ayuda a su imaginación e intuición. Supongo que uno se acostumbra con el uso a este tipo de conceptos abstractos.

El teorema de Emmy Noether, que relaciona magnitudes físicas conservadas con la invariancia ante simetrías continuas (grupos de Lie) en un sistema físico (clásico o cuántico), nos muestra que el espín y el momento angular tienen un origen común. Por ello, sus unidades y sus propiedades son similares (sus componentes están evaluadas en un álgebra de Lie), por lo que se pueden sumar (dando lugar al llamado momento orbital). De hecho, el operador de spín es un pseudovector (vector axial) como lo es el momento angular , es decir, bajo rotaciones se comporta como un vector ordinario, pero no cambia ante simetrías (reflexiones especulares) en el espacio.
La función de onda de una partícula tiene componentes  indexadas por el valor del espín cuyos valores discretos son  (para una partícula de espín ), es decir, tiene un valor para cada punto del espacio y para cada valor de la componente del vector de espín (donde es la proyección ortogonal del vector de espín en dicho eje de coordenadas). Una partícula de espín cero tiene una función de onda con una sola componente . Una partícula de espín 1/2 tiene una función de onda con dos “componentes” y . Y así sucesivamente. ¿”Componentes” entre comillas? La invariancia relativista de la ecuación de Dirac exige que la función de onda cuántica para un electrón tenga cuatro componentes en dos parejas, es decir, que sea un biespinor compuesto de dos espinores. En general, las componentes de la función de onda para partículas de espín semientero son espinores, a diferencia de las componentes “vectoriales” de las de espín entero. Esta diferencia, de origen matemático debido a las leyes de la relatividad combinadas con la mecánica cuántica, parece extraña y casi imposible de entender a quien ignora los detalles matemáticos. Un físico lo único que puede decir es que la Naturaleza es así. Mientras no tengamos una explicación a por qué la Naturaleza es cuántica y relativista no podremos explicar el origen último de estas propiedades. En el momento presente aún estamos muy alejados de poder entender por qué la Naturaleza es cuántica y relativista.
¿Por qué la función de onda tiene que ser descrita mediante una representación de un grupo? El principio más fundamental de la mecánica cuántica es que los estados de un sistema forman parte de un espacio de Hilbert (un espacio vectorial con un producto interior que es completo). No sabemos por qué, pero así es la Naturaleza. La descripción matemática de la acción de un grupo de simetría sobre un espacio de Hilbert requiere utilizar una representación, es decir, requiere describir las transformaciones del grupo como matrices que se multiplican por los vectores del espacio de Hilbert. La teoría de la representación de grupos es muy abstracta, pero su importancia es capital en física cuántica. En matemáticas, una representación de un grupo G es un homomorfismo de G en el grupo D(G) cuyos elementos son operadores en una espacio vectorial L (eligiendo una base de L los elementos de D(G) son matrices); L es el llamado espacio de representación y su dimensión es el grado (o dimensión) de la representación de D(G). Hay muchos tipos de representaciones de grupos, pero en física cuántica se utilizan representaciones unitarias, en las que las matrices son unitarias (matrices cuya inversa es igual a su adjunta conjugada y que preservan el producto interior del espacio de Hilbert).
Dado un campo, sea , dos observadores en sendos sistemas inerciales conectados por una transformación de Lorentz-Poincaré  (en componentes ) deben observar el mismo campo ; la covariancia relativista exige que el campo (es decir, la física) sea el mismo, aunque sea observado desde puntos de vista diferentes. Sin embargo, no tiene por qué cumplirse que . En general, si el campo tiene varias componentes, dichas componentes podrán “mezclarse” haciendo que , donde es una matriz que “representa” la transformación de Lorentz-Poincaré ; en componentes podemos escribir que . El tipo y las propiedades de las matrices depende del grupo de simetría considerado; para el grupo de Lorentz-Poincaré dichas matrices están caracterizadas por una propiedad, el espín, que relaciona las propiedades de estas matrices con el número de “componentes” del campo. La teoría de la representación de grupos de simetría se desarrolló a principios del s. XX junto a la mecánica cuántica (su nicho natural), aunque sus orígenes se pueden encontrar en la segunda mitad del s. XIX cuando los matemáticos estudiaron los orígenes de la geometría y su relación con los grupos de simetría.
Profundizar en estas cuestiones matemáticas quizás nos llevaría demasiado lejos. Cuando la gente me pregunta por qué los físicos no saben explicar con palabras sencillas lo que es el espín, yo suelo contestar que entender el espín es tan difícil como entender el momento angular. Hay libros enteros dedicados al momento angular, sus propiedades y cómo operar con él en sistemas multipartícula (algunos ejemplos en Google Books). No es fácil manejar el momento angular y el espín utilizando la intuición física clásica, por lo que la mayoría de los físicos trabajamos estos conceptos de forma operativa, obviando imágenes que nos confundan. Con el uso uno acaba teniendo la sensación de que los entiende, pero quizás sea solo una ilusión. Lo que debe quedar claro al lector es que las reglas matemáticas para manejar el momento angular y el espín en los cálculos están perfectamente claras y que, además, no existe ninguna analogía clásica que reproduzca todas y cada de una de estas reglas matemáticas; en los últimos 90 años ningún físico y ningún matemático ha logrado una analogía clásica adecuada que permite entender al lego estos conceptos tan abstractos y a la vez tan importantes. Repito, todas las analogías clásicas fallan (al menos las que yo he podido leer). Por cierto, hay algunas analogías clásicas “buenas” para ciertos valores del espín, pero no funcionan para todos.
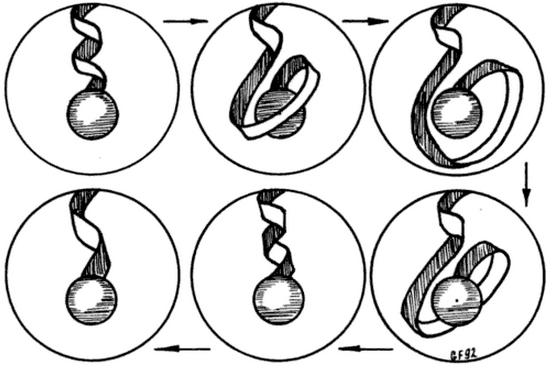
Para finalizar, las figuras que acompañan esta entrada corresponden al “truco del cinturón de Dirac” (también llamada “cinta de Dirac”) para explicar por qué un electrón tiene que “girar” 720 grados para recuperar su estado original (cuando para un objeto clásico basta un giro de 360 grados). Hay muchos vídeos de youtube, pero a mí me gusta el siguiente (que no explicaré en detalle). Os animo a profundizar usando Google, si os apetece.

Algunas referencias clásicas:
[1] Naturwissenschaften  13: 953-954, 1925; Nature 117: 264-265, 1926.
[2] Zeitschrift für Physik 43: 601-623, 1927.
[3] Proc. Roy. Soc. Lond. A 117: 610-624, 1928; Proc. R. Soc. Lond. A 118: 351-361, 1928.
[4] Gruppentheorie (Friedrich Vieweg und Sohn, Braunschweig, Germany, 1931), pp. 251-254.
[5] Math. Zeitschrift 23: 271-309, 1925; Math. Zeitschrift 24: 328-376, 1926; Math. Zeitschrift 24: 377-395, 1926; Math. Zeitschrift 24: 789-791, 1926.