
Introducción
Es bien sabido que la luz, o fotones, pueden orbitar alrededor del agujero negro de Schwarzschild en constante radio r = 3 M, donde M es la masa del agujero negro. Aunque tal órbita es inestable, no es menos importante desde el punto de vista físico, ya que define el límite entre la captura y la no captura de una muestra representativa de los rayos de luz por el agujero negro de Schwarzschild. Este límite ha jugado un papel importante en la determinación, por ejemplo, el aspecto que tendría el cielo nocturno para un observador cerca de un agujero negro estático o estrella de neutrones [ 1 ]. En el caso de un agujero negro en rotación Kerr, hay dos órbitas circulares de fotones que pudieran existir en el plano ecuatorial. Se trata de una órbita progrado moviéndose en la misma dirección que la rotación del agujero negro, mientras que la otra es una órbita retrógrada movimiento contra la rotación del agujero negro. Sus radios se recogen, respectivamente por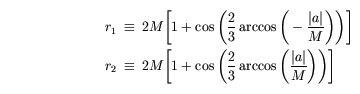
donde a es el momento angular por unidad de masa del agujero negro. Tenga en cuenta que en el límite de giro cero, estas dos órbitas coinciden en r = 3 M, dando a la órbita circular única del agujero negro de Schwarzschild.
Tal vez se conoce con menos frecuencia que las órbitas esféricas - es decir, las órbitas con radios constantes que no se limitan al plano ecuatorial - de fotones también son posibles alrededor de un agujero negro de Kerr. Tales órbitas fueron estudiados por primera vez en el caso de tipo temporal por Wilkins [ 2 ] hace algunos años. Aquí, voy a considerar la posibilidad de que las órbitas de fotones esféricas que generalizan las dos órbitas circulares antes mencionadas. Sus propiedades se discuten brevemente, y los modelos `malla de alambre" de órbitas seleccionadas se producen con la ayuda de un applet de Java. Espero que usted se sorprenderá de lo que tengo con los posibles patrones que estas órbitas se pueden trazar en el espacio tridimensional.
Existencia y propiedades de las órbitas fotónicas esféricas
Para deducir la existencia de órbitas de fotones esféricas, tenemos que considerar las ecuaciones geodésicas que rigen el movimiento de las partículas nulos alrededor de un agujero negro de Kerr. Resulta que se pueden escribir como un conjunto de cuatro ecuaciones diferenciales de primer orden, y una solución de estas ecuaciones se determina en función de tres constantes de movimiento: la energía del fotón, su momento angular alrededor del eje de rotación de la agujero negro, y la constante de Carter. Este último está relacionado con la velocidad angular del fotón en la dirección latitudinal, cuando se está pasando a través del plano ecuatorial (ver Ref.. [ 3 ] o las referencias en él). Se demostró en la ref. [ 3 ] que, para órbitas con radio constante r, la ecuación geodésica relevante puede ser resuelto a dar una clase de un parámetro de soluciones parametrizados en términos de r: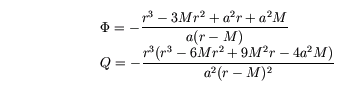
donde Phi y Q son constantes de movimiento proporcional al momento angular del fotón y constante de Carter, respectivamente. Estas soluciones son físicos, solamente si Q es positivo [ 3 ], que restringe r para el rango de 1 r <r <r 2. En cada extremo de este rango, Q se desvanece, dando los dos órbitas ecuatoriales mencionados anteriormente. Al igual que con las órbitas, estas soluciones son inestables bajo las perturbaciones radiales.
El siguiente gráfico muestra el comportamiento general de la phi y Q en función de r:
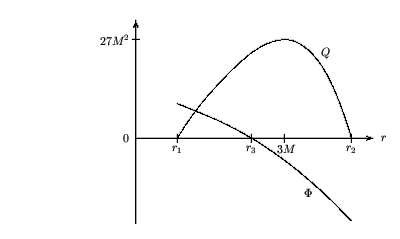
Como se puede ver, Q aumenta monotónicamente desde cero en r = r 1, a un valor máximo de 27 M 2 en r = 3 M, antes de monótonamente decreciente de nuevo a cero en r = r 2. Por otro lado, Phi disminuye monotónicamente desde algún valor positivo en r = r 1, a un valor negativo en r = r 2. Se desvanece en el radio intermedio:
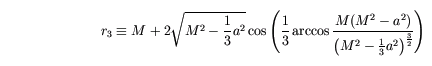
Órbitas con Phi positivo son prograda, mientras que aquellos con Phi negativo son retrógrada.
Otras propiedades de estos fotones órbitas esféricas se pueden deducir de las ecuaciones geodésicas. Por ejemplo, es posible mostrar que la latitud máxima que los fotones pueden alcanzar depende inversamente de | Phi |. En particular, pueden llegar a los polos norte y sur, si y sólo si Phi desvanece. También es posible obtener una expresión analítica para el cambio en el azimut de los fotones 'para una oscilación completa latitudinal de la órbita. Para más información sobre estas y otras propiedades, se remite al lector a Ref. [ 3 ].
Los ejemplos de las órbitas fotónicas esféricas
Para obtener ejemplos explícitos de estas órbitas esféricas de fotones, las ecuaciones geodésicas deben integrarse numéricamente. Esto se hizo con el cuarto orden algoritmo de Runge-Kutta. En cada uno de los siguientes ejemplos, las órbitas se representan en una esfera imaginaria de radio fijo. Cada órbita comienza en el ecuador y se dirige hacia el sur. El observador se supone que se encuentra a 30 ° al oeste del punto de partida de la órbita, y 60 ° al norte del ecuador. El sentido de rotación del agujero negro en sí es de oeste a este desde el punto de vista del observador.Por simplicidad, consideraremos sólo el caso de un agujero negro de Kerr extrema, es decir, cuando a = M. (Órbitas para un <M resultan ser cualitativamente similar, véase la tabla completa de ejemplos a continuación). En este caso, Phi toma el rango permitido físicamente -7 M <Phi <2 M.
Empezamos con el caso especial de la phi = 0 (que corresponde a r = r 3), que describe un fotón con momento angular cero. A pesar de esto, un fotón como todavía puede orbitar alrededor del agujero negro en radio constante debido al arrastre de marcos inerciales a su alrededor, según lo predicho por el conocido efecto Lense-Thirring . Además, como Phi desvanece, la órbita de los fotones se llevará a través de todas las latitudes posibles, derecho de los polos norte y sur. La siguiente figura muestra dos oscilaciones latitudinales de esta órbita:
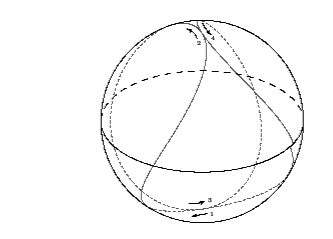
Para mayor claridad, flechas numeradas indican el orden y la dirección de movimiento. Al hacer clic sobre la figura da un modelo de alambre tridimensional de esta órbita, que puede ser examinado desde cualquier ángulo (pruébalo!).
Nuestro siguiente ejemplo, la phi = -2 M (r = 3 M), también es especial en el sentido de que es la órbita única que tiene el valor máximo permitido de Q, a saber, 27 M 2. Esto implica que el fotón se mueve verticalmente siempre que sea en el ecuador [ 3 ], un hecho que se desprende de la figura siguiente muestra tres oscilaciones latitudinales de esta órbita:
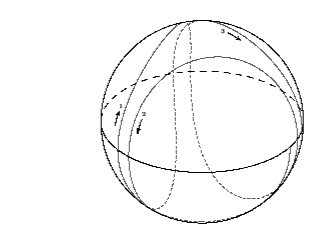
En general, sin embargo, es una órbita retrógrada con momento angular negativa. Este comportamiento se puede entender desde el efecto Lense-Thirring: el arrastre de marcos inerciales es más fuerte en el ecuador, y en este caso, se cancela precisamente el movimiento retrógrado del fotón. Lejos del ecuador, el arrastre se vuelve más débil y por lo tanto la órbita recupera su carácter retrógrado.
Cuando -2 M <Phi <0 (r 3 <r <3 M), resulta que las órbitas de fotones no tienen una dirección azimutal fijo. Cinco oscilaciones latitudinales para el caso de la phi = - M se muestra en la siguiente figura:
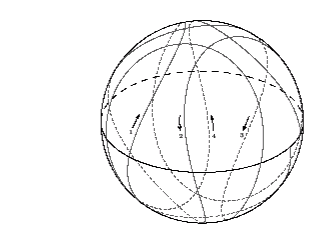
Observe que aunque la órbita está retrógrado, en general, se está moviendo realmente en la dirección progrado dentro de una cierta latitud del ecuador. De nuevo, esto se puede atribuir a la fuerza del efecto Lense-Thirring en la región ecuatorial: en este caso, el momento angular negativa de la fotón no es lo suficientemente grande como para negar este efecto, lo que resulta en que se arrastra a lo largo en la dirección de la rotación del agujero negro.
Por el momento angular -7 M <Phi <-2 M (3 M <r <r 2), las órbitas son completamente retrógrada incluso en la región ecuatorial. Esto es debido a que el momento angular del fotón es ahora lo suficientemente grande como para dominar sobre el efecto Lense-Thirring. Cuatro oscilaciones latitudinales para el caso de la phi = -6 M se muestra en la siguiente figura:
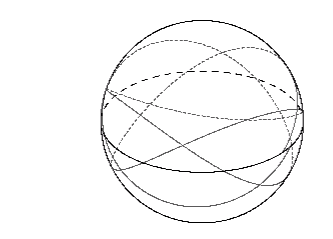
Otro punto a destacar de esta figura, es la relativamente baja latitud máxima del fotón. Se va a cero a medida que se acerca Phi -7 M, lo que resulta en una órbita circular retrógrada en el plano ecuatorial.
Pasamos ahora brevemente para el caso cuando Phi es positivo: 0 <Phi <2 M (r 1 <r <r 3), correspondiente a Prograde órbitas. Como un ejemplo, una oscilación latitudinal de la órbita con Phi = M se ilustra a continuación:
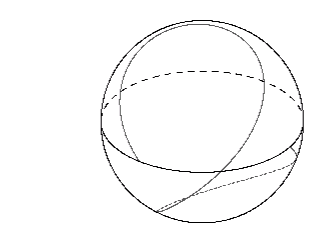
Como se puede ver, los cambios de fotones a la vuelta de tanto en el sur y el polo norte, teniendo más de una vuelta alrededor del agujero negro en completar una oscilación en la latitud. Un ejemplo más extremo es el caso de Phi = 1,999 M:
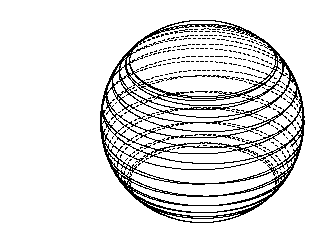
en el que un patrón helicoidal es aparente. El ángulo de inclinación del fotón ahora es tan pequeña que se necesita más de 25 revoluciones para completar la una oscilación en latitud.
Por último, cabe señalar que algunos patrones cuasi-periódicas en lugar interesantes resultaría si se continúan las órbitas de fotones anteriores para muchas oscilaciones latitudinales. Estos y otros ejemplos se pueden encontrar siguiendo el enlace de abajo. Disfrute!
Tabla completa de Ejemplo Órbitas
Referencias
[1] RJ Nemiroff (1993) `` distorsiones visuales cerca de una estrella de neutrones y agujero negro,'' American Journal of Física 61, 619-632. [ http://antwrp.gsfc.nasa.gov/htmltest/rjn_bht.html ] [2] DC Wilkins (1972) `` geodésicas Bound en la métrica de Kerr,'' Physical Review D 5, 814-822.[3] E. Teo (2003) `` órbitas fotones esféricos alrededor de un agujero negro de Kerr,'' la Relatividad General y Gravitación 35, 1909-1926. [ ps , pdf ]